2025年高职单招每日一练《数学(中职)》4月26日专为备考2025年数学(中职)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、如图,在四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN//平面PAD,则()
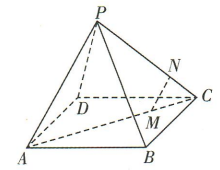
- A:MN//PD
- B:MN//PA
- C:MN//AD
- D:以上均有可能
答 案:B
解 析:∵MN//平面PAD,MN⊂平面PAC,平面PAD∩平面PAC=PA,∴根据线面平行的性质定理可得MN//PA.
2、已知A,B,C三个社区的居民人数分别为600,1200,1500,现采用比例分配的分层随机抽样的方法抽取一个容量为n的样本,若从C社区抽取了15人,则n=()
- A:33
- B:18
- C:27
- D:21
答 案:A
解 析:因为A,B,C三个社区的居民人数分别为600,1200,1500,按分层随机抽样的方法抽取一个容量为n的样本,且C社区抽取了15人,所以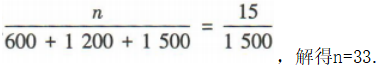
3、设集合A={a,b,c,d},B={b,d,e,f},则A∩B=()
- A:{b,d}
- B:{b}
- C:{a,b,c,d,e,f}
- D:∅
答 案:A
解 析:因为A={a,b,c,d},B={b,d,e,f},所以A∩B={b,d}.
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、已知△ABC中,∠A,∠B,∠C所对边为a,b,c,C=30°,a=c=2,则b=____.
答 案:2√3
解 析:a=c=2, 所以A=C=30°,B=120°, 所以b2=a2+c2-2accosB=12, 所以b= 2√3
2、(2+x)6展开式中含x3项的二项式系数为()
答 案:20
解 析:(2+x)6展开式中含x3项的二项式系数为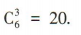
3、过点P(2,-1),且与直线3x-2y+5=0垂直的直线方程是()
答 案:2x+3y-1=0
解 析:设与直线3x-2y+5=0垂直的直线方程为2x+3y+C=0,将点P(2,-1)代入可得2 x2+3x(-1)+C=0,解得C=-1,所以所求直线方程为 2x+3y-1= 0.
简答题
1、设△ABC的内角A,B,C的对边分别为a,b,c,且a=2,b=3, (1)求sinC的值;
(2)求cos(A+B)+sin2C的值.
(1)求sinC的值;
(2)求cos(A+B)+sin2C的值.
答 案: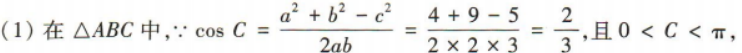
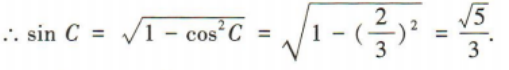
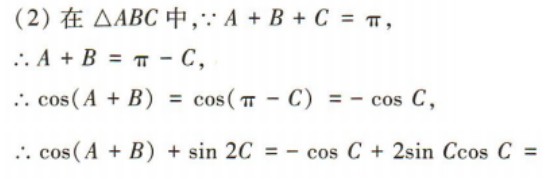

精彩评论