2025年高职单招每日一练《数学》4月27日专为备考2025年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、方程x²+y²=9表示圆心在原点，半径为3的一个圆。（）  

答 案：对

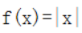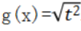2、函数与表示同一个函数。（）  

答 案：对

解 析：f(x)=|x|和g(x)=根号下是同一函数.
因为它们的定义域相同,都是R.
它们的对应规律相同,即自变量的绝对值等于函数值.
函数的两个要素均相同.
所以,它们是同一函数.
此外,它们的图象完全重合.
注意两点：
1.函数关系（特别提示：仅仅指函数关系）与表示自变量和函数的字母无关.
2.当我们比较两个函数关系异同的时候,往往是先化简,再比较.
如函数y＝x/x与u＝t⁰,分别化简为y＝1,且x≠0；u＝1,t≠0.按上述考察,它们是同一函数.
从形式上看,前者是分式函数,后者是幂函数.
“形式”是入门的向导,入门以后应抓住“本质”.
化简以后,也就是把它们的面纱揭去以后,原来它们是同一个函数.
最后,f(x)=|x|和g(x)=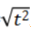不是同一函数.特别注意后者g(x)明明白白表示g是自变量x的函数.而根号下中是否含有x,不得而知.

单选题

1、等腰三角形的一个内角是50°，则这个三角形的底角的大小是()  

• A：65°或50°
• B：80°或40°
• C：65°或80°
• D：50°或80°

答 案：A

解 析：当50°的角是底角时，三角形的底角就是50°；当50°的角是顶角时，两底角相等，根据三角形的内角和定理易得底角是65度

2、 下列函数中，在区间(0,1)是增函数的是（）  

• A：Y=|X+1|
• B：Y=2-X
• C：Y=
• D：Y=X²-X+1

答 案：A

解 析：利用一次函数，二次函数，反比例函数的单调性逐一分析即可在(0,1)上y=| x+1|=x+1,单调递增;y=2-x单调递减y=在(0,+∞)上单调递减,故在(0,1)上单调递减上单调递减;在y =x'-x+1在（-∞，1/2）上单调递减，在（1/2,+∞）上单调递增,故在(0.1)上不是单调递增函数故选:A本题考查简单函数的单调性，属基础题，熟练掌握一次函数，反比例函数，二次函数的单调性是解决此问题的关键

多选题

1、已知数列{3n-1}，下面选项正确的是（）  

• A：这个数列是公比为3的等比数列
• B：这个数列是公差为3的等差数列
• C：这个数列的第5项是14
• D：20是这个数列的第7项

答 案：BCD

解 析：已知数列{3n-1}，这个数列是公差为3的等差数列，故A错误，B正确。数列第五项=3*5-1=14。故C正确。数列第七项=3*7-1=20.故D正确

2、下列计算结果正确的是（）  

• A：
• B：
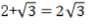
• C：
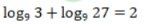
• D：

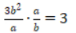
答 案：AC

主观题

1、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

2、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

填空题

1、一个圆柱和一个圆锥的底面直径和它们的高都与某一个球的直径相等，这时圆柱、圆锥、球的体积之比为______  

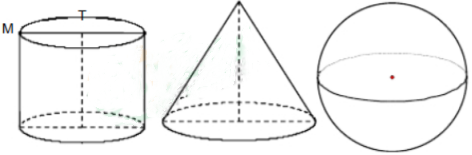
答 案：3:1:2

2、函数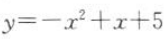的单调增区间是（）.

答 案：

解 析：函数的图像开口向下，对称轴是直线,则其单调增区间是