2025年高职单招每日一练《数学(中职)》4月27日专为备考2025年数学(中职)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、若α:x2=4,β:x=2,则α是β的()
- A:充分不必要条件
- B:必要不充分条件
- C:充要条件
- D:既不充分也不必要条件
答 案:B
解 析:易知x2=4,解得x=±2.显然x=2可以推出x2=4,但x2=4不能推出x=2,所以α是β的必要不充分条件
2、现从4名男生和3名女生中,任选3名男生和2名女生,分别担任5门不同学科的课代表,则不同的安排方法的种数是
- A: 12
- B:120
- C:1 440
- D:17 280
答 案:C
解 析:第一步,从4名男生和3名女生中任选3名男生和2名女生,不同选法共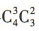 种,第二步,选出的5个人分别担任5门不同的学科代表,不同的安排方法共
种,第二步,选出的5个人分别担任5门不同的学科代表,不同的安排方法共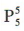 种,由分步乘法计数原理知不同的安排方法共有
种,由分步乘法计数原理知不同的安排方法共有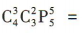
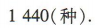
3、已知A(0,2),B(4,-8),则线段AB的中点坐标为()
- A:(-2,-3)
- B:(2,3)
- C:(-2,3)
- D:(2,-3)
答 案:D
解 析:因为A(0,2),B(4,-8),所以线段AB的中点坐标为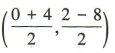 ,即(2,-3).
,即(2,-3).
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、某高中学校三个年级共有学生2000名.若在全校学生中随机抽取一名学生,抽到高二年级女生的概率为 0.19,则高二年级的女生人数为()
答 案:380
解 析:易得高二年级的女生人数为2000x0.19=380.
2、某企业操作岗位、技术岗位和管理岗位的人数分别是 700,210,140.为了解该企业不同岗位员工的健康状况,采用分层抽样的方法,从这三个岗位的所有员工中随机抽取 300 人进行体检,则应从操作岗位抽取的人数是()
答 案:200
解 析:因为操作岗位人数与员工总数的比为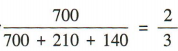 ,所以应从操作岗位抽取的人数是 300x
,所以应从操作岗位抽取的人数是 300x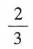 = 200.
= 200.
3、设△ABC的内角A,B,C的对边分别为a,b,c,已知4a=3b,B=2A,则cosA=()
答 案: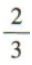
解 析: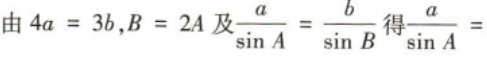

简答题
1、若bc-ad≥0,bd>0,证明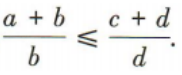
答 案: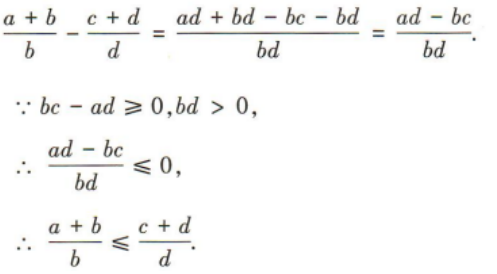
精彩评论