2025年高职单招每日一练《数学(中职)》4月30日专为备考2025年数学(中职)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、若ln2 =m，ln5 = n,则，e^m+2n的值是（）  

• A：2
• B：5
• C：50
• D：20

答 案：C

2、已知tanα=-3,则cos²α-sin²α=()  

• A：
• B：
• C：
• D：

答 案：B

解 析：因为tanα=-3,所以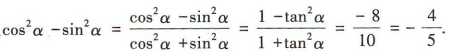

3、经过椭圆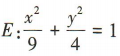的左焦点的直线1与椭圆E交于A,B两点,F是椭圆E的右焦点,则△ABF的周长为()  

• A：4
• B：6
• C：12
• D：18

答 案：C

解 析：设椭圆E的左焦点为F₁,由题意及椭圆的定义得|AF₁|+|AF|=2a=6,|BF₁|+|BFl= 2a=6,所以△AABF的周长为|AB|+|AF|+|BF|=|AF₁|+|BF₁|+|AF|+|BF|= 12.

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、函数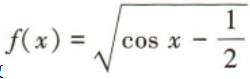的定义域为（）

答 案：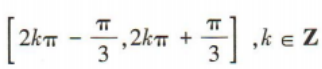

解 析：

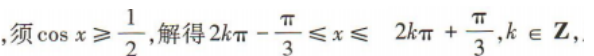
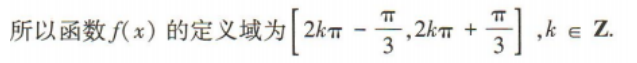
2、(2+3i)-(4 +5i)=（）.(其中i是虚数单位)  

答 案：-2-2i

解 析：易得(2+3i)-(4+5i)=-2-2i.

3、将某校100名学生的数学测试成绩绘制成如图所示的频率分布直方图,分数不低于a(a为整数)为优秀,如果优秀的人数为20,则a的估计值是()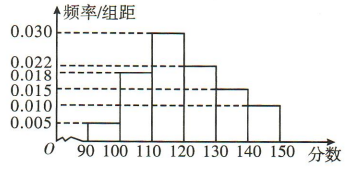  

答 案：133

解 析：分数低于140的人数为100x10x(0.005+0.018+0.030+0.022+0.015)= 90.分数低于130的人数为100 x10x(0.005 +0.018 + 0.030+0.022)= 75,故a∈(130,140),所以[(140-a) x0. 015 + 0.01 x 10]x100=20.解得a≈133.

简答题

1、解方程:x²-x+1=0.  

答 案：由x²-x+1=0得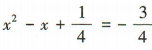，即 ∴方程x²-x+1=0的两根分别为