2025年高职单招每日一练《数学(中职)》5月7日专为备考2025年数学(中职)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知△ABC的内角A,B,C的对边分别为a,b,c,若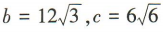 ,B=45°,则C=()
,B=45°,则C=()
- A:30°
- B:105°
- C:150°
- D:30°或105°
答 案:A
解 析:在△ABC中,由 ,得
,得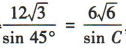 ,解得
,解得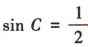 .因为
.因为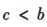 ,所以
,所以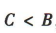 ,所以C=30°.
,所以C=30°.
2、已知向量a,b满足|a|=2,|bl=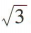 ,且a与b的夹角为30°,那么a·b=()
,且a与b的夹角为30°,那么a·b=()
- A:1
- B:
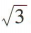
- C:3
- D:
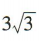
答 案:C
解 析: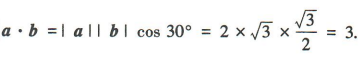
3、某记者要去武汉4个医院采访,则不同的采访顺序有
- A:4 种
- B:12 种
- C:18 种
- D:24 种
答 案:D
解 析:由题意可得不同的采访顺序有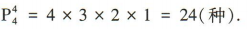
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、如图,A,B两点在河的两岸,在B同侧的河岸边选取点C,测得BC的距离为10,∠ABC=75°,∠ACB=60°,则A,B两点间的距离为()
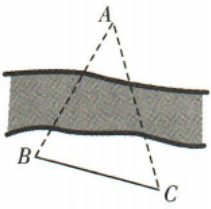
答 案: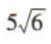
解 析:
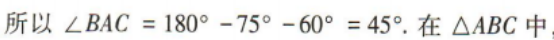
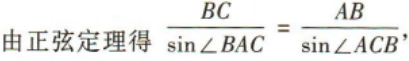
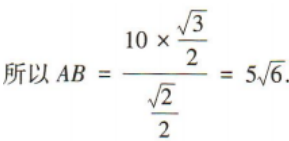
2、两平行直线l1:3x+4y+2=0与l2:3x+4y-1=0之间的距离是()
答 案: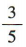
解 析:直线l1:3x+4y+2=0与l2:3x+4y-1=0之间的距离为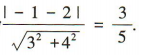
3、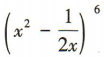 展开式中的常数项为()
展开式中的常数项为()
答 案: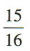
解 析:易知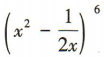 展开式的通项为
展开式的通项为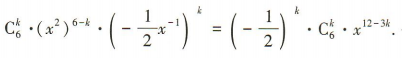 令12-3k =0,解得k=4,所以
令12-3k =0,解得k=4,所以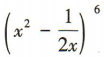 展开式中的常数项为
展开式中的常数项为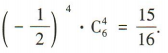
简答题
1、已知集合 A={x|6x2+mx-1=0},B={x|3x2+5x+n=0},且A∩B={-1},求AUB
答 案:解:因为A∩B={-1},所以−1∈A且-1∈B
由-1∈A得6-m-1=0,m=5
得A={x|6x2+5x−1=0}=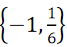 由-1∈B得3-5+n=0,n=2
得B={x|3x2+5x+2=0}=
由-1∈B得3-5+n=0,n=2
得B={x|3x2+5x+2=0}=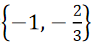 所以
所以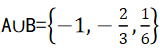
精彩评论