2025年高职单招每日一练《数学(中职)》5月25日专为备考2025年数学(中职)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、已知a=(-1,2),b=(3,m),且|a+b|=|a-b|,则m=（）

• A：
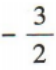
• B：
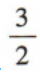
• C：6
• D：-6

答 案：B

解 析：由a=(-1,2),b=(3,m),得a+b=(2,2+m),a-b=(-4,2-m),又|a+b|=|a-b|,所以4+(2+m)²=16+(2-m)²,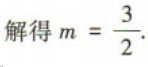

2、已知向量a=(2,0),b=(1,1),则（）

• A：|a|=|b|
• B：(a-b)//b
• C：(a-b)⊥b
• D：

答 案：C

解 析：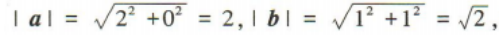

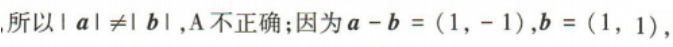
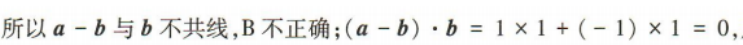
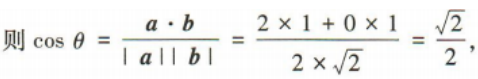
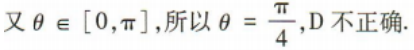
3、圆心为(-2,3),半径为2的圆的方程是（）  

• A：(x-2)²+(y+3)²=2
• B：(x+2)²+(y-3)²=4
• C：(x+2)²+(y-3)²=2
• D：(x-2)²+(y+3)²=4

答 案：B

解 析：圆心为(-2,3),半径为2,∴圆的标准方程为(x+2)²+(y-3)²=4.

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、(x-2)⁶的展开式中x⁴的系数为()  

答 案：60

解 析：(x-2)⁶的展开式的通项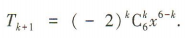令6-k=4，可得k=2.则x⁴的系数是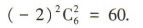

2、等比数列{a}中,已知a1+a4=9,a2+a5=18,则S5=（）  

答 案：31

解 析：设等比数列{an}的公比为q.因为a1+a4=9,所以a2+a5=q(a1+a4)=9q=18,解得q=2,所以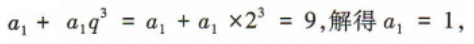

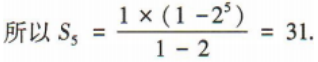
3、过点P(2,-1),且与直线3x-2y+5=0垂直的直线方程是()  

答 案：2x+3y-1=0

解 析：设与直线3x-2y+5=0垂直的直线方程为2x+3y+C=0,将点P(2,-1)代入可得2 x2+3x(-1)+C=0,解得C=-1,所以所求直线方程为 2x+3y-1= 0.

简答题

1、计算不定积分∫(2e^x-x+cosx)dx.  

答 案：解：原式=2e^x-1/2x²+sinx+C