2025年高职单招每日一练《数学(中职)》6月10日专为备考2025年数学(中职)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、直线3x-y-1=0的斜率k及在y轴上的截距b分别是()
- A:k=3,b=-1
- B:k=-3,b=1
- C:
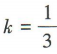 ,b=1
,b=1 - D:k=3,b=1
答 案:A
解 析:由直线3x-y-1=0得y=3x-1,所以直线的斜率k=3,在y轴上的截距b=-1.
2、下列各角中,与440°角终边相同的角是()
- A:280
- B:160°
- C:-80°
- D:-280°
答 案:D
解 析:与440°角终边相同的角为α=440°+360°·k,k∈Z.结合选项可得当k=-2时,α=-280°符合题意.
3、若sinθ<0,cosθ<0,则θ是()
- A:第一象限角
- B:第二象限角
- C:第三象限角
- D:第四象限角
答 案:C
解 析:由sinθ<0,得θ的终边在第三象限或第四象限或与y轴负半轴重合.由cosθ<0,得θ的终边在第二象限或第三象限或与x轴负半轴重合.综上,θ是第三象限角。
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、已知{an}是首项a1=1.公差d=3的等差数列,若an=2005.则n等于()
答 案:669
解 析:因为等差数列{an}的首项a1=1,公差d=3,所以an=1+3(n-1)=3n-2,由3n-2=2005可得n=669.
2、3(2a-b)-5(a+3b)=()
答 案:a-18b
解 析:3(2a-b)-5(a+3b)=6a-3b-5a-15b=(6-5)a-(3+15)b=a-18b.
3、已知点P在圆x2+(y-1)2=9上,若点P到直线y=x+1的距离为3,则满足条件的点P的个数为()
答 案:2
解 析:易知圆x2+(y-1)2=9的圆心为(0,1),半径r=3.因为直线y=x+1经过圆心,且点P到直线y=x+1的距离为3=r,所以满足条件的点P的个数为2.
简答题
1、计算不定积分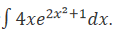
答 案:解:原式=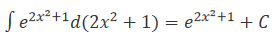
精彩评论