2025年成考高起点每日一练《数学(理)》3月14日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、下列函数中，为偶函数的是（）。

• A：
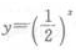
• B：
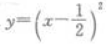
• C：
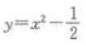
• D：

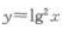
答 案：C

解 析：根据函数的奇偶性的定义可知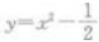为偶函数

2、已知2^a=3，2^b=6，2^C=12，则（）.  

• A：b²=a+c
• B：2b=ac
• C：2b=a+c
• D：b²=ac

答 案：C

解 析：由已知，2^a·2^c=36，即2^a+c=36。又（2^b）²=6²，2^2b=36，则2^2b=2^a+c，2b=a+c选C。

3、i为虚数单位，则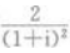的值为（）。

• A：1
• B：－1
• C：i
• D：－i

答 案：D

解 析：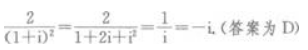

4、双曲线的渐近线方程为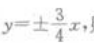则该双曲线的离心率为（）。

• A：
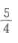
• B：2
• C：
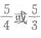
• D：

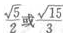
答 案：C

解 析：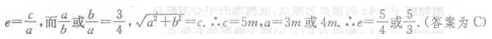

主观题

1、已知一组数据9.9；10.3；9.8；10.1；10.4；10；9.8；9.7，计算这组数据的方差。  

答 案：

2、空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  

答 案：根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式所以共可确定四个平面。

解 析：空间有n个点，如果其中任何三点不在同一直线上，可以确定个平面。  

3、在△ABC中如果sinA=2sinBcosC，求证：△ABC是等腰三角形。  

答 案：∴△ABC为等腰三角形。

4、记△ABC的内角A，B，C的对边分别为a，b，c，已知B=60°，b²=ac，求A。    

答 案：由余弦定理b²=a²+c²-2accosB，可得ac=a²+c²-ac，即a²+c²-2ac=(a-c)²=0，解得a=c。 又因为B=60°，故△ABC为等边三角形，所以A=60°

填空题

1、sin²10°+sin²20°+sin²40°+sin²50°+sin²70°+sin²80=______。

答 案：3

解 析：由互为余角的余函数值相等得 原式=(sin²10°+cos²10°)+(sin²20°+cos²20°)+(sin²40+cos²40)=1+1+1=3

2、cos²67.5°- 0.5=______。

答 案：

解 析：