2025年成考高起点每日一练《数学(文史)》3月14日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、与圆x2+y2=4关于点M（3,2）成中心对称的曲线方程是（）

• A：（x-3）2+（y-2）2=0
• B：（x+3）2+（y+2）2=0
• C：（x-6）2+（y-4）2=0
• D：（x+6）2+（y+4）2=0

答 案：C

解 析：与圆关于点M成中心对称的曲线还是圆.只要求出圆心和半径，即可求出圆的方程.圆X2+y2=4的圆心(0，0)关于点M(3,2)成中心对称的点为(6,4),所以所求圆的圆心为(6,4),半径与对称圆的半径相等，所以所求圆的方程为(x-6)2+(y-4)2=4。  

2、设集合P=（1，2，3，4，5），Q={2，4，6，8，10}，则集合P∩Q=（）。  

• A：｛2，4}
• B：｛1，2，3，4，5，6，8，10}
• C：｛2｝
• D：｛4｝

答 案：A

3、已知函数f(x)的定义域为R，且满足f(2x)=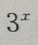,则f(x)的反函数为（）

• A：
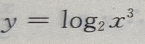
• B：
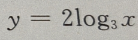
• C：
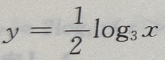
• D：

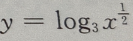
答 案：B

解 析：令2x=t，则x=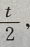  

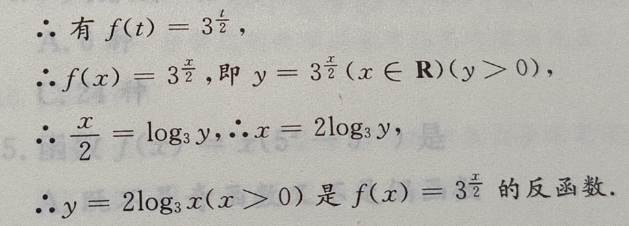
4、直线2x-y+7=0,与圆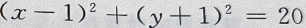的位置关系是（）  

• A：相离
• B：相交但不过圆心
• C：相切
• D：相交且过圆心

答 案：C

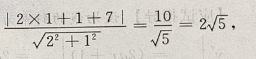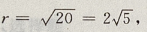解 析：易知圆心坐标（1，-1），圆心到直线2x-y+7=0的距离d ∵圆的半径 ∴d=r，∴直线与圆相切  

主观题

1、一艘渔船在航行中遇险，发出警报，在遇险地点西南10海里处有一艘货轮，接收到报时，发现遇险渔船正以9海里/小时的速度与沿南偏东75°方向向某小岛靠近，如果要在40分内将这艘渔船救出，求货轮航行的方向和速度。

答 案：货轮沿东偏北21.8°的方向，以21海里/小时的船速航行。

2、如图9-4，已知测速站P到公路L的距离为40米，一辆汽车在公路L上行驶，测得此车从A点行驶到8点所用的时间为2秒，并测得∠APO=60°，∠BPO=30°，计算此车从A到B的平均速度为多少km/h（结果保留到个位），并判断此车是否超过了80km/h的限制速度。

答 案：此车从A到B的平均速度为83（km/h），已经超过80km/h的限制速度。

3、在△ABC中，已知AB=2,BC=1,CA=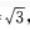 点D,E,F分别在AB,BC,CA边上，△DEF为正三角形，记∠FEC为α，如果sinα= 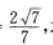求△DEF的边长。

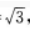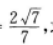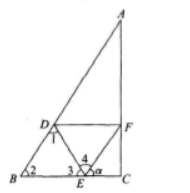
答 案：解析:由AB=2，BC=1,CA= 得BC²=CA²=AB²,因此∠C=90°，如图所示。 因为sinA= 所以∠A=30°，于是∠b=60°。 设正△DEF边长为l，已知AB=2,sinα= 由此EC=lcosα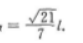 有图知，∠1+∠2+∠3=180°（三角形内角和）； ∠3+∠4+α=180°，因为∠2-∠4=60°，所以∠1=α。 【考点指要】本题主要考查三角函数的概念、同角三角函数的关系及正弦定理，这些均是考试大纲要求掌握的重要概念，并要求能达到灵活应用的程度，此类题是在成人高考中出现频率较高的题型，

4、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。  

答 案：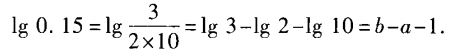

填空题

1、设则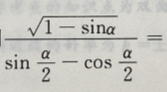

答 案：-1

解 析：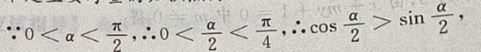  

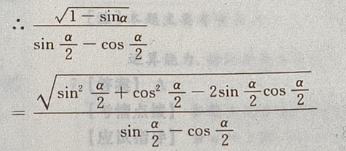
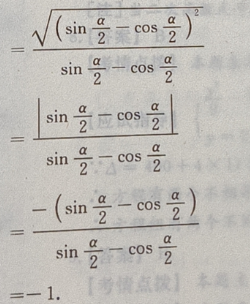
2、“a＞b”是“a-c＞b-c”的______。

答 案：充要条件