2025年成考高起点每日一练《数学(文史)》3月16日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设α是第一象限角，则sin2α=（）。

• A：
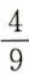
• B：
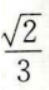
• C：
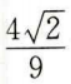
• D：

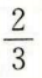
答 案：C

解 析：本题主要考查的知识点为三角函数的二倍角公式。 α在第一象限，则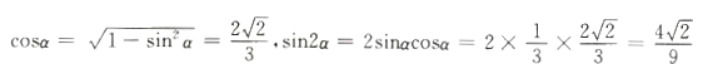

2、下列函数中，为奇函数的是（）。  

• A：y=x³
• B：y=-x³-1
• C：
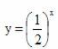
• D：

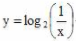
答 案：A

3、若|a|=|b|=1，且a⊥b，又2a+3b与λa-4b互相垂直，则λ为（）

• A：6
• B：-6
• C：3
• D：-3

答 案：A

4、不等式-2x²+3＜5x的解集是（）。  

• A：空集
• B：{x|-3＜x＜}
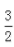• C：全体实数
• D：{x|x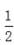＞或x＜-3}

答 案：D

解 析：-2x²+3＜5x解：2x²-3＜-5x2x²-3+5x＞0
根据十字交叉法：
（2X-1）（X+3）＞0
解得为D  

主观题

1、已知a,b,c成等比数列，x是a，b的等差中项，y是b，c的等差中项证明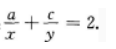  

答 案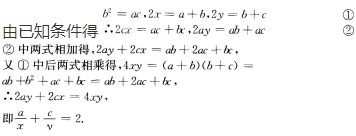： 考点 本题考查考生对等差中项和等比中项公式的理解及运用．

2、设全集U=R，集合A={x｜-5＜x＜5}，B={x｜0≤x≤7}，求CUA∩B．

答 案：解：全集U=R，A={x｜-5＜x＜5}，B=｛X｜0≤x≤7}，因为CuA={x｜x≤-5或x≥5}，所以CuA∩B={x｜x≤-5或x≥5}N{x｜0≤x≤7}={x｜5≤x≤7}，如图1—10所示。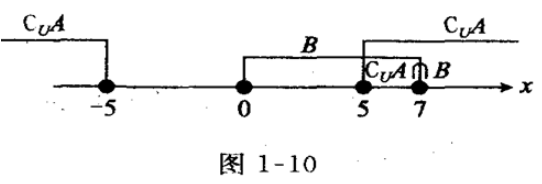

3、已知函数f（x）=（x-4）（x2-a）。（I）求f’（x）；
（Ⅱ）若f’（-1）=8，求f（x）在区间[0，4]的最大值与最小值。

答 案：(I)f'(x) =(x-4)'(x²-a)+(x-4)(x²-a)’ =x²-a+2x(x-4) =3x²-8x-a. (Ⅱ)由于f’(-1)=3+8-a=8,得a=3. 令f'(x)=3x²-8x-3=0,解得x1=3，（舍去）又f（0）=12，f（3）=-6，f（4）=0所以在区间[0，4]上函数最大值为12，最小值为-6

4、求下列函数的最大值、最小值和最小正周期： （1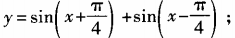） 2）y=6cosx+8sinx

答 案： 所以函数的最大值是最小值是最小正周期为2π， （2）要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式，需使cosx与sinx的系数平方和为1，为此，将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π

填空题

1、在∆ABC中，已知cosA=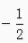，cosB=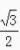，那么cosC=______。

答 案：

2、平面内有10个点，任何三点都不在同一直线上，问能连成______条不同的直线。  

答 案：45