2025年成考高起点每日一练《数学(文史)》3月19日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知3sin2α+8sinα-3=0,则cos2α=()。
- A:
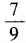
- B:
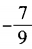
- C:
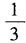
- D:
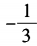
答 案:A
解 析:由已知得(3sinα-1)(sinα+3)=0。 由于|sinα|≤1,所以sinα=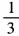 。因此
。因此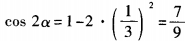 。故选A。
。故选A。
2、已知向量a=(3,1),b=(-2,5),则3a-2b=()。
- A:(2,7)
- B:(13,-7)
- C:(2,-7)
- D:(13,,13)
答 案:B
解 析:根据a=(3,1),b=(-2,5),则3a-2b=3×(3,1)-2×(-2,5)=(13,-7)
3、cos12°cos98°-sin12°sin98°=()。
- A:cos20°
- B:sin20°
- C:-cos20°
- D:-sin20°
答 案:D
解 析:原式=cos110°=cos(180°-70°)=-cos70°=-cos(90°-20°)=-sin20°。
4、一射击手独立射击8次,每次中靶的概率是0.7,那么恰好中靶5次的概率是()。
- A:
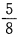
- B:
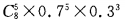
- C:
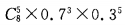
- D:
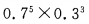
答 案:B
解 析:此题试验属于独立重复试验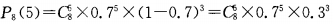 ,故应选B。
,故应选B。
主观题
1、若双曲线 的两条准线将两个焦点的连线分成三等分,求双曲线的离心率。
的两条准线将两个焦点的连线分成三等分,求双曲线的离心率。
答 案:设双曲线的半焦距为c,则双曲线 【考点指要】本题要求根据双曲线的焦距、离心率、准线方程三者之间的关系进行计算,属较容易题,在成人高考中常见.
【考点指要】本题要求根据双曲线的焦距、离心率、准线方程三者之间的关系进行计算,属较容易题,在成人高考中常见.
2、等差数列{an}的通项公式为an=3n-1,在{an}中,每相邻的两项之间插人三项,构成新的等差数列{bn}. (Ⅰ)求{bn}的通项公式; (Ⅱ)求{bn}前10项的和.
答 案: 考点本题主要考查等差数列的通项公式和前n项和公式的运用,是成人高考常见题型.
考点本题主要考查等差数列的通项公式和前n项和公式的运用,是成人高考常见题型.
3、每亩地种果树20棵时,每棵果树收入90元,如果每亩增种一棵,每棵果树收入就下降3元,求使总收入最大的种植棵数.
答 案:设每亩增种x棵,总收入味y元,则每亩种树(20+x)棵,由题意知增种x棵后每棵收入为(60-3x) 则有y=(90-3x)(20+x)
整理得y=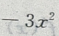 +30x+1800
配方得y=
+30x+1800
配方得y= +1875
当x=5时,y有最大值,所以每亩地最多种25棵
+1875
当x=5时,y有最大值,所以每亩地最多种25棵
4、在△ABC中,已知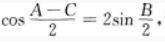 证明a,b,c成等差数列。
证明a,b,c成等差数列。
答 案: 考点 本题主要考查三角函数的恒等变换以及积化和差公式的应用,积化和差有一定难度,请考生注意.
考点 本题主要考查三角函数的恒等变换以及积化和差公式的应用,积化和差有一定难度,请考生注意.
填空题
1、直线 的倾斜角的度数为()
的倾斜角的度数为()
答 案:60°
解 析:由题意知直线的斜率为 设直线的倾斜角为α,则tanα=
设直线的倾斜角为α,则tanα= 由0°≤α≤180°,故α=60°
由0°≤α≤180°,故α=60°
2、袋中装有3个白球,2个红球,从中任取2个球,取到2个都是红球的概率是______。
答 案:
解 析: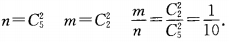
精彩评论