2025年成考高起点每日一练《数学(理)》3月20日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、函数y=sinx+cosx(x∈R)的最小正周期为()。
- A:2π
- B:π
- C:
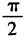
- D:
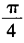
答 案:A
解 析: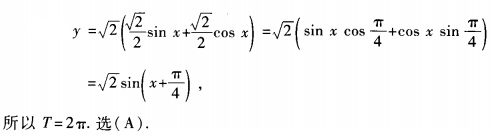
2、设f(x)=x3+ax2+x为奇函数,则a=()。
- A:1
- B:0
- C:
- D:-2 D.C.-1
答 案:B
解 析:本题主要考查的知识点为函数的奇偶性. 因为f(x)为奇函数,故f(-x)=-f(x)。即-x3+ax2-x=-x3-ax2-x,a=0。
3、函数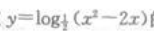 的定义域是()。
的定义域是()。
- A:(-∞,0)∪[2,+∞)
- B:[0,2]
- C:(-∞,0)∪(2,+∞)
- D:(0,2)
答 案:C
解 析:x2-2x>0,解得x<0或x>2.函数的定义域为(-∞,0)∪(2,+∞)。答案为C。
4、已知球的大圆周长是π,则这个球的表面积是()。
- A:
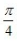
- B:4π
- C:2π
- D:π
答 案:D
主观题
1、已知A(1,4),B(3,8),C(4,10)。求证A、B、C三点共线。
答 案: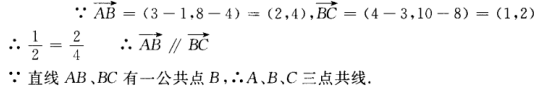
2、试证明下列各题
(1)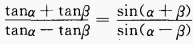
(2)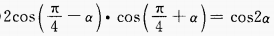
答 案:(1)化正切为正、余弦,通分即可得证。 (2)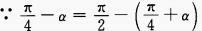

3、当自变量为何值时,函数y=2x3-3x2-12x+21有极值,其极值为多少?
答 案:y'=6x2-6x-12=6(x-2)(x+1) 当x<-1或x>2时,y>0,当-1
4、已知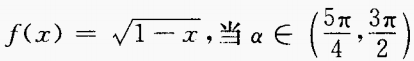 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。
答 案:由已知得, 填空题 1、九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。
答 案:85
解 析:本题主要考查的知识点为中位数. 将成绩按由小到大排列:63,77,79,81,85,88,89,94,99.因此中位数为85。 2、lgsinθ=a,lgcosθ=b,则sin2θ=______。
答 案:2×10a+b 解 析: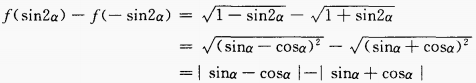
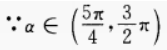 ∴sinα
∴sinα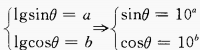 sin2θ=2sinθcosθ=2×10a×10b=2×10a+b
sin2θ=2sinθcosθ=2×10a×10b=2×10a+b
精彩评论