2025年成考高起点每日一练《数学(理)》3月23日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、若 ,则下列不等式成立的是()。
,则下列不等式成立的是()。
- A:
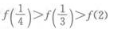
- B:
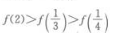
- C:
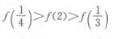
- D:

答 案:A
解 析: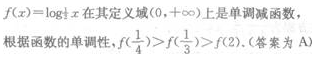
2、函数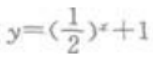 的值域是()。
的值域是()。
- A:(0,+∞)
- B:(-∞,+∞)
- C:(1,+∞)
- D:[1,+∞)
答 案:C
解 析:
3、已知点M(1,2),N(2,3),则直线MN的斜率为()。
- A:
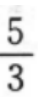
- B:1
- C:
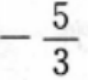
- D:-1
答 案:B
解 析:本题主要考查的知识点为直线的斜率.
直线MN的斜率为: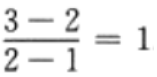
4、在定义域内下列函数中为增函数的是()。
- A:f(x)=2-x
- B:f(x)=-log2x
- C:f(x)=x3
- D:f(x)=x2+1
答 案:C
解 析:由函数的性质可知,f(x)=x3为增函数。(答案为C)
主观题
1、已知log53=a,log54=b,求log2512关于a,b的表达式。
答 案: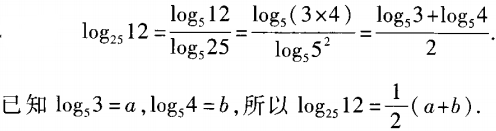
2、设a为实数,且tanα和tanβ是方程ax2+(2a-3)x+(a-2)=0的两个实根,求tan(α+β)的最小值。
答 案:由已知得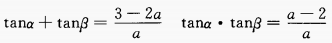

3、空间有四个点,如果其中任何三点不在同一直线上,可以确定几个平面?
答 案:根据公理,在所给定的四点中任取三点,可确定一个平面,由组合公式 所以共可确定四个平面。
所以共可确定四个平面。
解 析:空间有n个点,如果其中任何三点不在同一直线上,可以确定 个平面。
个平面。
4、已知函数f(x)=(x-4)(x2-a) (I)求f"(x); (Ⅱ)若f"(-1)=8,求f(x)在区间[0,4]的最大值与最小值
答 案: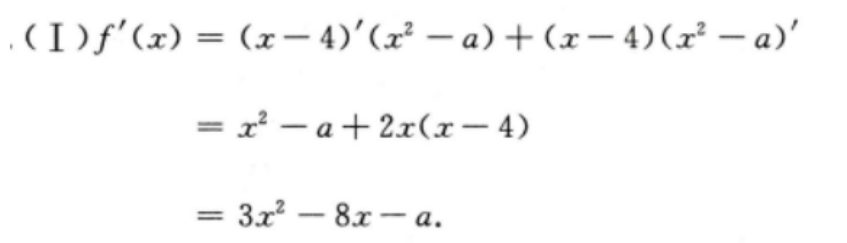

填空题
1、在自然数1、2、…、100中任取一个数,该数能被3整除的概率是______。
答 案:0.33
解 析:此题随机试验包含的基本事件总数n=100,且每个数能被取到的机会均等,即属于等可能事件的概率能被3整除的自然数的个数m=33,故所求概率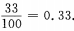
2、函数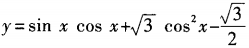 (x∈R)的最小值为______。
(x∈R)的最小值为______。
答 案:-1
解 析: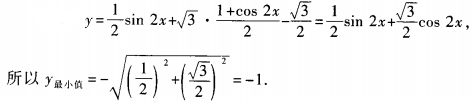
精彩评论