2025年成考高起点每日一练《数学(文史)》3月27日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、点(2,4)关于直线y=x的对称点的坐标为（）  

• A：(4,2)
• B：(-2,-4)
• C：(-2,4)
• D：(-4,-2)

答 案：A

解 析：点(2,4) 关于直线y=x对称的点为(4,2)

2、从15名学生中选出两人担任正、副班长，不同的选举结果共有（）  

• A：30种
• B：90种
• C：210种
• D：225种

答 案：C

解 析：由已知条件可知本题属于排列问题，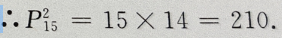

3、某车间有甲、乙两台机床，已知甲机床停机的概率为0.06，乙机床停机的概率为0.07，甲、乙两车床同时停机的概率是（）。

• A：0.13
• B：0.0042
• C：0.03
• D：0.04

答 案：B

4、已知集合A={0，1，2，3，4}，B={x|0＜x＜4}，则A∩B=（）。  

• A：{0，1，2，3}
• B：{1，2，3}
• C：{1，2}
• D：{0，4}

答 案：B

主观题

1、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积

答 案：

2、设椭圆的中心是坐标原点,长轴在x轴上,离心率已知点P到圆上的点的最远距离是求椭圆的方程  

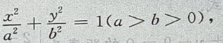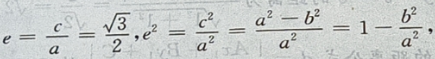
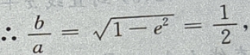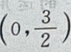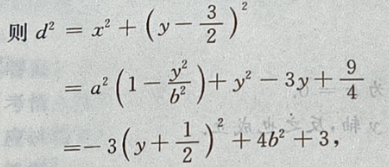
答 案：由题意，设椭圆方程为 由 设P点到椭圆上任一点的距离为 d, 则在y=-b时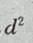，最大，即d也最大。  

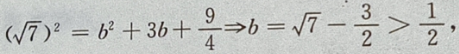
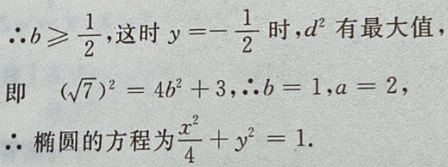
3、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。

答 案：(I)由题意,该抛物线的焦点到准线的距离为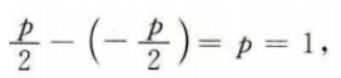 所以抛物线C的方程为y²=2x. (Ⅱ)因A(l,m)(m>0)为C上一点,故有m²=2, 可得 m=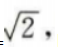因此A点坐标为 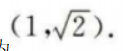设B点坐标为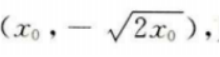

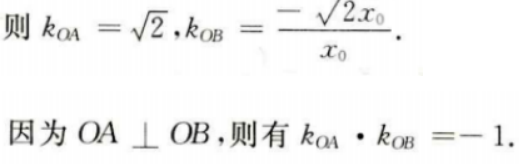
4、已知三角形的一个内角是，面积是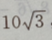周长是20,求各边的长.  

答 案：设三角形三边分别为a,b,c,∠A=60°，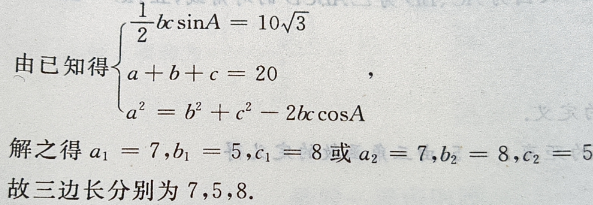  

填空题

1、已知点P（-3，1）为角α终边上一点，则cos（2α-π）的值等于______。  

答 案：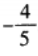

解 析：因为cos（2α-π）=cos（π-2α）=-cos2α。由已知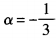， 所以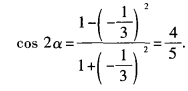

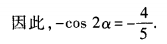
2、已知关于t的二次方程t²-6tsinθ+tanθ=0（0＜θ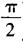＜）的两根相等，则sinθ+cosθ的值等于______。  

答 案：

解 析：