2025年成考高起点每日一练《数学(理)》4月12日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、在△ABC中，c-acosB=（）。

• A：bcosA
• B：acosC
• C：bcosB
• D：ccosA

答 案：A

解 析：由余弦定理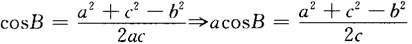

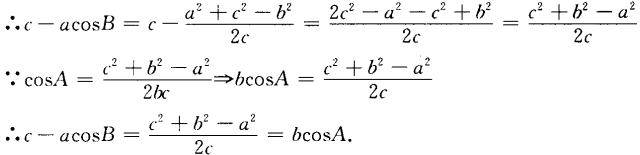
2、（ ）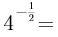

• A：-2
• B：
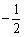
• C：
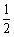
• D：2

答 案：C

3、过直线3x＋2y＋1＝0与2x－3y＋5＝0的交点，且垂直于直线L：6x－2y＋5＝0的直线方程是（）。

• A：x－3y－2＝0
• B：x＋3y－2＝0
• C：x－3y＋2＝0
• D：x＋3y＋2＝0

答 案：B

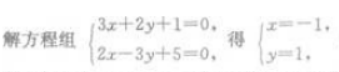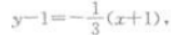解 析： 即两直线的交点坐标为（-1,1） 又直线L:6x-2y+5=0的斜率为3 ，则所求的直线方程为即x+3y-2=0.

4、如果点A(1，1)和B(2，4)关于直线y=kx+b对称，则k=（）。

• A：-3
• B：
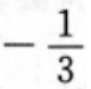
• C：
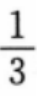
• D：3

答 案：B

解 析：本题主要考查的知识点为两垂直直线斜率的关系。直线AB的斜率为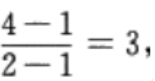点A、B关于直线y=kx+b对称，因此直线AB与其垂直，故3k=-1，得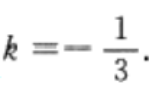

主观题

1、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得AB=120m,求河的宽

答 案：如图， ∵∠C=180°-30°-75°=75° ∴△ABC为等腰三角形，则AC=AB=120m 过C做CD⊥AB,则由Rt△ACD可求得CD==60m， 即河宽为60m  

2、cos20°cos40°cos80°的值。

答 案：

3、在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.

答 案：由△ABC的面积为得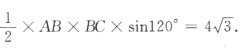所以AB =4.因此所以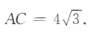

4、空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  

答 案：根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式所以共可确定四个平面。

解 析：空间有n个点，如果其中任何三点不在同一直线上，可以确定个平面。  

填空题

1、已知≤0＜2π，且实数x满足log₃x=2-cos²θ+sin²θ，则x的最小值是______。  

答 案：3

解 析：因为log₃x=2-（cos²θ-sin²θ）=2-cos2θ。 又log₃x中的底数3＞1，因此要使x最小，应使2-cos2θ的值最小，而其最小值为1，故x=3。

2、函数y=x⁴-2x²+5,x∈[-2,2]上的最小值______，最大值______。

答 案：4；13

解 析：y=x⁴-2x²+5,y'=4x³-4x