2025年成考高起点每日一练《数学(文史)》4月13日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知M为椭圆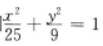 上的一点,F1,F2是椭圆的两个焦点,且∠F1MF2=60°,则△F1MF2的面积为()
上的一点,F1,F2是椭圆的两个焦点,且∠F1MF2=60°,则△F1MF2的面积为()
- A:
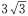
- B:3
- C:
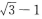
- D:
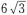
答 案:A
解 析:由椭圆方程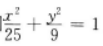 知,长轴长2a=10,焦距2c=8,设|MF1|=t,由余弦定理82=t2+(10-t)2-2t(10-t)cos60°,得
知,长轴长2a=10,焦距2c=8,设|MF1|=t,由余弦定理82=t2+(10-t)2-2t(10-t)cos60°,得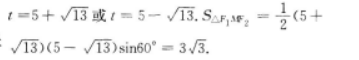
2、直线l1与直线l2:3x+2y-12=0的交点在x轴上,并且l1⊥l2,则l1在y轴上的截距是()。
- A:-4
- B:

- C:4
- D:

答 案:B
解 析:由于直线l2:3x+2y-12=0与x轴的交点为(4,0),斜率为 故直线l1的斜率为
故直线l1的斜率为 ,且经过(4,0),故l1的方程为y-0=
,且经过(4,0),故l1的方程为y-0= 令x=0求得
令x=0求得 ,即l1在y轴上的截距是
,即l1在y轴上的截距是 故选C。
用点斜式求得直线l1的方程,再根据直线在y轴上的截距的定义求得l1在y轴上的截距,本题主要考查用点斜式求直线的方程,直线在y轴上的截距的定义和求法,属于基础题
故选C。
用点斜式求得直线l1的方程,再根据直线在y轴上的截距的定义求得l1在y轴上的截距,本题主要考查用点斜式求直线的方程,直线在y轴上的截距的定义和求法,属于基础题
3、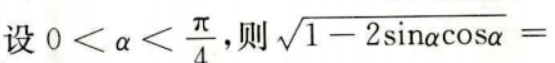 ()。
()。
- A:sinα+cosα
- B:-sinα—cosα
- C:sinα—cosα
- D:cosα—sinα
答 案:D
解 析:本题主要考查的知识点为三角函数的运算。 当时,cosα>sinα>0,所以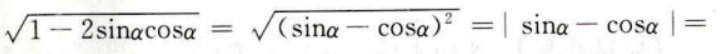
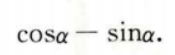
4、函数y=sinx+cosx(x∈R)的最小正周期为()。
- A:2π
- B:π
- C:
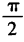
- D:
答 案:A
解 析: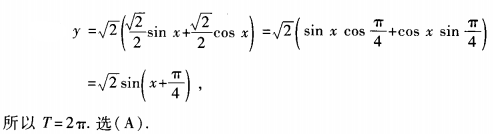
主观题
1、已知三角形的三边边长组成公差为1的等差数列,且最大角是最小角的二倍,求三边之长。
答 案:三角形的三边边长分别为4,5,6。
2、设3a=5b=15,求a-1+b-1的值。
答 案:由3a=15,得a=log315;又由5b=15,得b=log515。 因此a-1+b-1=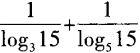 =log153+log155=1。
=log153+log155=1。
解 析:过程中应用了换底公式的推论,即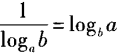
3、设函数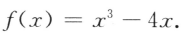
(I)求f'(2);
(II)求f(x)在区间[一1,2]的最大值与最小值.
答 案:(I)因为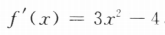 ,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.
,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.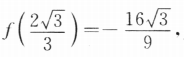 f(2)=0.
f(2)=0.
所以f(x)在区间[一1,2]的最大值为3,最小值为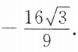
4、若tanα、tanβ是关于x的方程mx2-(2m-3)x+m-2=0的两个实根,求tan(α+β)的取值范围
答 案: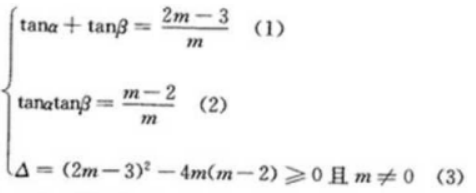 由(1)(2)得,tan(a+β)=m-3/2;由(3)得m≤9/4且m≠0所以tan(a+β)的取值范围是(-∞,-3/2)U(-3/2,3/4)
由(1)(2)得,tan(a+β)=m-3/2;由(3)得m≤9/4且m≠0所以tan(a+β)的取值范围是(-∞,-3/2)U(-3/2,3/4)
填空题
1、已知tanθ=1/2,则sin2θ+sin2θ=__________.
答 案:1
解 析:
2、5个同学站成一排,其中某个人恰好站在排头的概率是______。
答 案: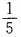
解 析:基本事件的总数n=5!,其中某人恰好站在排头的排法有m=4!种,所求概率为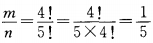 。
。
精彩评论