2025年成考高起点每日一练《数学(理)》4月15日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、若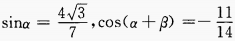 ,且α、β均为锐角,则β的值为()。
,且α、β均为锐角,则β的值为()。
- A:
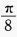
- B:
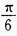
- C:
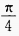
- D:
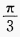
答 案:D
解 析:
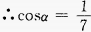
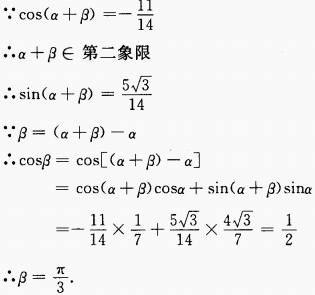
2、二次函数y=2x2+mx-5在区间(-∞,-1)内是减函数,在区间(-1,+∞)内是增函数,则m的值是()。
- A:4
- B:-4
- C:2
- D:-2
答 案:A
解 析:由题意可知二次函数y=2x2+mx-5的对称轴方程为x=-1,又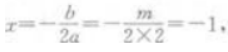 解得m=4
解得m=4
3、曲线y=x+2在点(1,2)处的切线斜率为()。
- A:1
- B:2
- C:-1
- D:4
答 案:A
解 析:方法一:∵y=x+2,k=y’=1 方法二:也可用直线方程y=kx+b直接得出k=1。
4、函数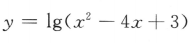 的定义域是()
的定义域是()
- A:{x|-3<x<-1}
- B:{x|x<-3或x>-1}
- C:{x|1<x<3}
- D:{x|x<1或x>3}
答 案:D
解 析:由对数函数的性质可知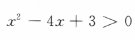 ,解得x>3或x<1,因此函数的定义域为{x|x<1或x>3}
,解得x>3或x<1,因此函数的定义域为{x|x<1或x>3}
主观题
1、在正四棱柱ABCD-A'B'C'D'中, (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证:
答 案:(Ⅰ)由题意知(如图所示) 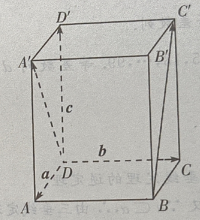
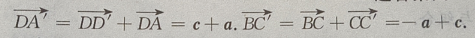
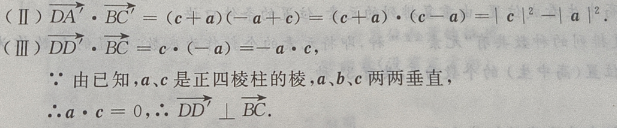
2、如图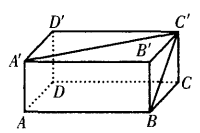 ,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?
,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?
(2)A’B’和DD’的距离是多少?
答 案:(1)在长方体中BC和A’C’不在同一个平面内 所以BC和A’C’是异面直线 ∵在长方体中BC//B’C’ ∴∠A’C’B’是异面直线BC和A’C’所成的角
∵A’C’B’=45°
异面直线BC和A’C’所成的角是45°
(2)A’B’和DD’是异面直线
∵A’D’⊥A’B’ A’D’⊥DD’
∴A’D’的长即为异面直线A’B’和DD’的距离
∵A’D’=4
∴A’B’和DD’间的距离为4cm。
3、计算。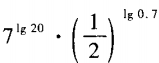
答 案: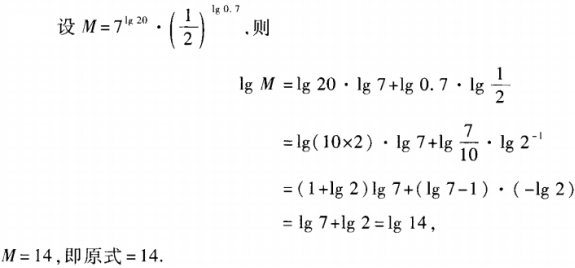
4、已知数列{an}中,a1=2,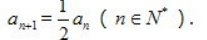 (Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
答 案:解:
填空题
1、ABCD是正方形,E是AB的中点,如将△DAE和△CBE分别沿虚线DE、CE折起,使AE与BE重合如图 ,设A与B重合后的点为P,则面PCD与面ECD所成的二面角为______度,PE与面ECD成______度。
,设A与B重合后的点为P,则面PCD与面ECD所成的二面角为______度,PE与面ECD成______度。
答 案:二面角为30°,PE与面ECS成60角°
解 析:(1)求面PCD与面ECD所成的二面角为多少度,就是要求出由平面PCD与平面ECD所组成的二面角的平面角,其中画出二面角的平面角是关键,因为二面角确定以后,二面角的平面角很容易画出(由二面角的平面角的定义)。求角度时,常用到勾股定理、正弦定理、余弦定理、兰垂线定理和逆定理。 (2)求PE与面ECD成多少度,就是求直线与平面所成的角是多少度。首先要找出平面的一条斜线(直线PE)和斜线的射影,斜线和射影所成的锐角,就是直线PE和平面ECD所成的角,再求出角度。 设CD的中点为F,练PF,EF
∵PC=PD,EC=ED.
∴PF⊥CD,EF⊥CD(三垂线定理)
∠PFE是二面角P-CD-E的平面角
∵PE⊥PC,PE⊥CD.
∴PE⊥平面PCD,又PF在平面PCD内
∴PE⊥PF
设正方形边长为1(如图)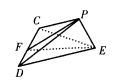
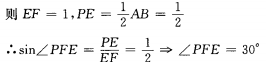 故面PCD与面ECD所成的二面角为30°,PE与面ECS成60角°。
故面PCD与面ECD所成的二面角为30°,PE与面ECS成60角°。
2、过点(2,0)作圆x2+y2=1的切线,切点的横坐标为()。
答 案: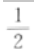
解 析:本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有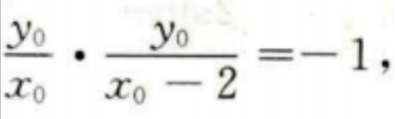 即
即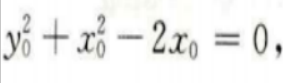
 所以
所以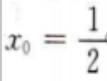 故切点横坐标为
故切点横坐标为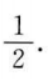
精彩评论