2025年成考高起点每日一练《数学(文史)》4月15日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、若函数y=f(x)在[-1,1]上是单调函数,则使得y=f(sinx)必为单调函数的区间是()  

• A：R
• B：[-1,1]
• C：
• D：[-sin1 ,sin1]

答 案：C

解 析：y=f(x)在[-1,1]上是单调函数,所以y=f(x)的单调区间为[-1,1]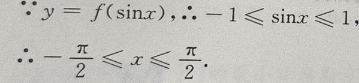  

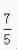2、已知sinα+cosα=，sinα-cosα=，则tanα等于（）。

• A：
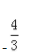
• B：
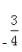
• C：1
• D：-1

答 案：A

3、一枚硬币连抛3次，至少有两次正面向上的概率是（）。

• A：
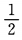
• B：
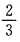
• C：
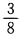
• D：

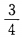
答 案：A

解 析：此题一枚硬币连抛3次等价于3枚硬币抛一次，这种试验的等可能结果总数n=8，其至少两次正面向上的结果总数m=4，故所求概率为，故应选A。

4、若|a|=|b|=1，且a⊥b，又2a+3b与λa-4b互相垂直，则λ为（）

• A：6
• B：-6
• C：3
• D：-3

答 案：A

主观题

1、在△ABC中，已知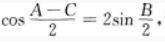证明a，b，c成等差数列。

答 案： 考点 本题主要考查三角函数的恒等变换以及积化和差公式的应用，积化和差有一定难度，请考生注意．

2、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积

答 案：

3、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。

答 案：(I)由题意,该抛物线的焦点到准线的距离为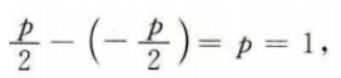 所以抛物线C的方程为y²=2x. (Ⅱ)因A(l,m)(m>0)为C上一点,故有m²=2, 可得 m=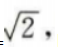因此A点坐标为 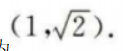设B点坐标为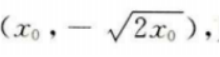

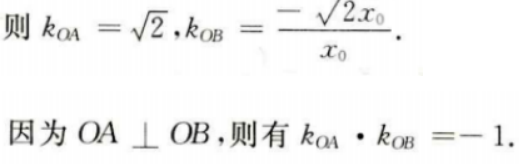
4、在△ABC中，B=120°,C=30°,BC=4，求△ABC的面积．

答 案：因为A= 180°-B-C=30°，所以AB = BC=4.因此△ABC的面积

填空题

1、已知5^a=2，25^b=9，则5^2a-b的值等于______。  

答 案：

解 析：由25^b=9，得5^2b=9，5^b=3。又5^a=2，则  

2、化简sin（x+y）-2cosxsiny=______。  

答 案：sin（x-y）

解 析：原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin（x-y）