2025年成考高起点每日一练《数学(理)》4月21日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、=（）。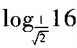

• A：8
• B：-8
• C：2
• D：-2

答 案：B

解 析：由于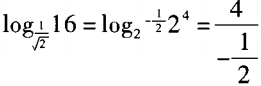。log₂2=-8。故选B。  

2、若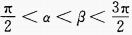，则必有（）。

• A：sinα＞sinβ
• B：cosα＞cosβ
• C：tanα＞tanβ
• D：cotα＞cotβ

答 案：A

解 析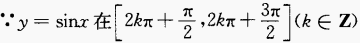： 是函数，故当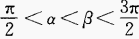时，  

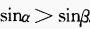
3、中心在坐标原点，一个焦点的坐标是（-3,0），一条渐近线方程式的双曲线方程是（）。

• A：
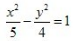
• B：
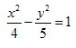
• C：
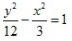
• D：

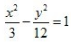
答 案：B

4、设f(x)=ax+b目f(0)=-2,f(3)=4,则f(2)=（）。

• A：6
• B：2
• C：1
• D：0

答 案：B

主观题

1、在△ABC中如果sinA=2sinBcosC，求证：△ABC是等腰三角形。  

答 案：∴△ABC为等腰三角形。

2、已知一组数据9.9；10.3；9.8；10.1；10.4；10；9.8；9.7，计算这组数据的方差。  

答 案：

3、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得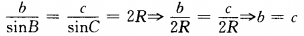

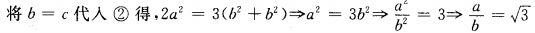
∴a：b=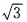：1
于是a：b：c=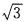：1：1。  

4、已知a,b,c成等差数列，a,b,c+1成等比数列．若b=6，求a和c．

答 案：由已知得解得

填空题

1、函数y=-x²+ax图像的对称轴为x=2，则a=______。  

答 案：4

解 析：本题主要考查的知识点为二次函数的性质 由题意，该函数图像的对称轴为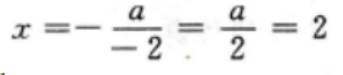

2、一个问题在1小时内，甲能独立解决的概率是0.5，乙能独立解决的概率是0.4，两人在1小时内解决问题的概率是______。  

答 案：0.7

解 析：设事件A为两人在1小时内解决问题，即1小时内至少有一人能解决问题，事件B为甲在1小时内解决问题，事件C为乙在1小时内解决问题，事件B、C是相互独立事件，事件A的对立事件 互为在1小时内两个人都没有解决问题，所以 P（A）=1-P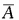（）=1-P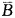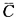（·）=1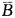-P（）·P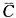（） =1-（1-0.5）×（1-0.4）=1-（0.5×0.6）=1-0.3=0.7