2025年成考高起点每日一练《数学(文史)》4月24日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、袋中有6个球，其中4个红球，2个白球，从中随机取出2个球，则这2个球都为红球的概率为（）

• A：
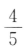
• B：
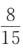
• C：
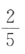
• D：

答 案：C

解 析：两个球都是红球的概率为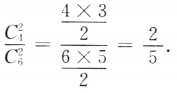

2、设集合M={1，2，3，4，5}，N={2，4，6}，T={4，5，6}则（M∩T）∪N是（）。  

• A：{2，4，5，6}
• B：{4，5，6}
• C：{1，2，3，4，5，6}
• D：{2，4，6}

答 案：A

3、已知tanα+sinα=m，tanα-sinα=n（m+n≠0），则cosα的值是（）。  

• A：
• B：
• C：
• D：

答 案：A

4、已知向量a=（3,1），b=（-2,5），则3a-2b=（）。

• A：（2,7）
• B：（13，-7）
• C：（2，-7）
• D：（13，,13）

答 案：B

解 析：根据a=(3,1),b=(-2,5),则3a-2b=3×(3,1)-2×(-2,5)=(13,-7)  

主观题

1、设椭圆的中心是坐标原点，长袖在x轴上，离心率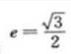，已知点P（0,3/2）到椭圆上的点的最远距离是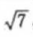，求椭圆的方程。

答 案：

2、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

3、已知a-a^-1=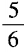，求a³-a^-3的值。  

答 案：

4、（1）已知tanα=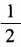 求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1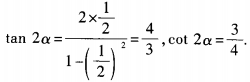） （2）由已知，得 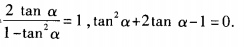解关于tanα的一元二次方程，得tanα=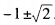

填空题

1、已知关于t的二次方程t²-6tsinθ+tanθ=0（0＜θ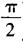＜）的两根相等，则sinθ+cosθ的值等于______。  

答 案：

解 析：

2、已知tanθ=1/2，则sin2θ+sin2θ=__________．

答 案：1

解 析：