2025年成考高起点每日一练《数学(理)》4月25日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、在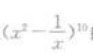的展开式中,含x⁵项的系数是（）。

• A：1
• B：-1
• C：252
• D：-252

答 案：D

解 析：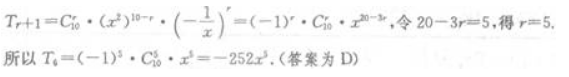

2、函数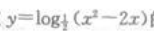的定义域是（）。

• A：(－∞，0）∪[2，＋∞)
• B：[0，2]
• C：(－∞，0)∪（2，＋∞)
• D：(0，2)

答 案：C

解 析：x²－2x＞0，解得x＜0或x＞2．函数的定义域为(－∞，0)∪(2，＋∞)。答案为C。

3、过直线3x＋2y＋1＝0与2x－3y＋5＝0的交点，且垂直于直线L：6x－2y＋5＝0的直线方程是（）。

• A：x－3y－2＝0
• B：x＋3y－2＝0
• C：x－3y＋2＝0
• D：x＋3y＋2＝0

答 案：B

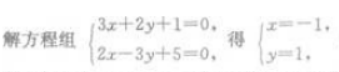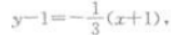解 析： 即两直线的交点坐标为（-1,1） 又直线L:6x-2y+5=0的斜率为3 ，则所求的直线方程为即x+3y-2=0.

4、若a＞b＞0，则（）。

• A：log2a
• B：2^a<2^b
• C：
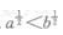
• D：

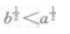
答 案：D

解 析：根据指数函数与对数函数的单调性可知,当a>b>0时,有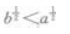恒成立

主观题

1、已知数列{a_n}中，a₁=2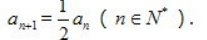， （Ⅰ）求数列{a_n}的通项公式; （Ⅱ）求数列{a_n}前5项的和 S₅

答 案：解：

2、已知一组数据9.9；10.3；9.8；10.1；10.4；10；9.8；9.7，计算这组数据的方差。  

答 案：

3、（1）已知tanα=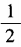，求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1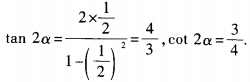）（2）由已知，得 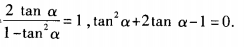解关于tanα的一元二次方程，得tanα=  

4、记△ABC的内角A，B，C的对边分别为a，b，c，已知B=60°，b²=ac，求A。    

答 案：由余弦定理b²=a²+c²-2accosB，可得ac=a²+c²-ac，即a²+c²-2ac=(a-c)²=0，解得a=c。 又因为B=60°，故△ABC为等边三角形，所以A=60°

填空题

1、在△ABC中，a=2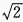，b=，∠B=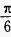，则∠A=______。

答 案：

解 析：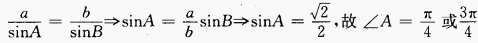

2、函数y=x⁴-2x²+5,x∈[-2,2]上的最小值______，最大值______。

答 案：4；13

解 析：y=x⁴-2x²+5,y'=4x³-4x