2025年成考高起点每日一练《数学(理)》4月28日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、给出下列两个命题：①如果一条直线与一个平面垂直，则该直线与该平面内的任意一条直线垂直②以二面角的棱上任意一点为端点，在二面角的两个面内分别作射线，则这两条射线所成的角为该二面角的平面角.则（）

• A：①②都为真命题
• B：①为真命题，②为假命题
• C：①为假命题，②为真命题
• D：①②都为假命题

答 案：B

解 析：一条直线与平面垂直，则直线与平面内的任意一条直线垂直，故①为真命题；二面角的两条射线必须垂直于二面角的棱，故②为假命题，因此选B选项．

2、直线l1与l2：3x + 2y - 12 =0 的交点在x轴上，且l1⊥l2，则l1在y轴的截距是（）。

• A：-4
• B：
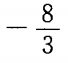
• C：4
• D：

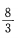
答 案：B

解 析：

3、设集合M={1,2,4}，N={2,3,5}，则集合M∪N=（）.

• A：{2}
• B：{1，2，3，4，5}
• C：{3，5}
• D：{1，4}

答 案：B

解 析：M∪N={1,2,4}∪{2,3,5)= {1，2，3，4，5} (答案为B)

4、已知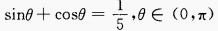，则cotθ的值是（）。

• A：
• B：
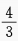
• C：
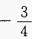
• D：

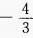
答 案：C

解 析：从已知式两边平方得到，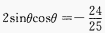

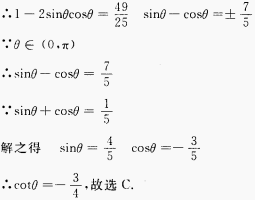
主观题

1、已知关于x的二次方程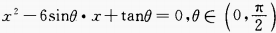的两根相等，求sinθ+cosθ的值。

答 案：

2、已知等差数列｛an｝中，a1+a2+a3=6,a2+a4+a5= 12求｛an｝的首项与公差。  

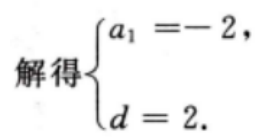
答 案：因为｛an｝为等差数列，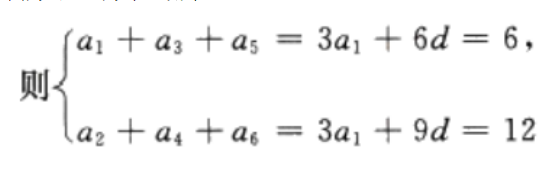

3、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得AB=120m,求河的宽

答 案：如图， ∵∠C=180°-30°-75°=75° ∴△ABC为等腰三角形，则AC=AB=120m 过C做CD⊥AB,则由Rt△ACD可求得CD==60m， 即河宽为60m  

4、已知a^m=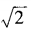，an=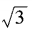，求a3^n-4m的值。  

答 案：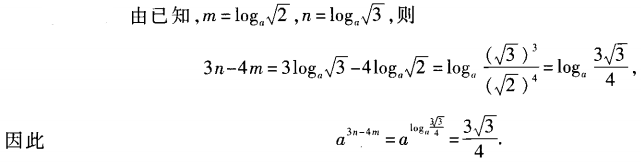

填空题

1、ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE、CE折起，使AE与BE重合如图 ，设A与B重合后的点为P，则面PCD与面ECD所成的二面角为______度，PE与面ECD成______度。

答 案：二面角为30°，PE与面ECS成60角°  

解 析：（1）求面PCD与面ECD所成的二面角为多少度，就是要求出由平面PCD与平面ECD所组成的二面角的平面角，其中画出二面角的平面角是关键，因为二面角确定以后，二面角的平面角很容易画出（由二面角的平面角的定义）。求角度时，常用到勾股定理、正弦定理、余弦定理、兰垂线定理和逆定理。 （2）求PE与面ECD成多少度，就是求直线与平面所成的角是多少度。首先要找出平面的一条斜线（直线PE）和斜线的射影，斜线和射影所成的锐角，就是直线PE和平面ECD所成的角，再求出角度。 设CD的中点为F，练PF，EF
∵PC=PD，EC=ED.
∴PF⊥CD，EF⊥CD（三垂线定理）
∠PFE是二面角P-CD-E的平面角
∵PE⊥PC，PE⊥CD.
∴PE⊥平面PCD，又PF在平面PCD内
∴PE⊥PF
设正方形边长为1（如图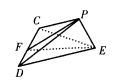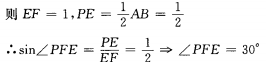） 故面PCD与面ECD所成的二面角为30°，PE与面ECS成60角°。

2、函数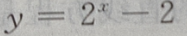的图像与坐标轴的交点共有（）  

答 案：2

解 析：当x=0时，y=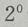-2=-1，故函数与y轴交于(0,-1)点，令y=0,则有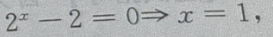故函数与x轴交于(1,0) 点,因此函数 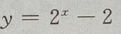与坐标轴的交点共有 2个.