2025年成考高起点每日一练《数学(文史)》5月10日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、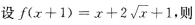 ( )
( )
- A:
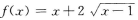
- B:

- C:
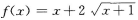
- D:
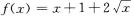
答 案:A
解 析:当已知ƒ(x+1)求ƒ(x)时,一般都用变量代换法,设x+1=t,则x=t-1,代入原式中得f(t)=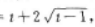 再将t换写成x即可
考点 本题主要考查函数的一般运算,如已知ƒ(x)求ƒ(x+1)或已知ƒ(x+1)求ƒ(x).
再将t换写成x即可
考点 本题主要考查函数的一般运算,如已知ƒ(x)求ƒ(x+1)或已知ƒ(x+1)求ƒ(x).
2、已知向量a=(3,1),b=(-2,5),则3a-2b=()。
- A:(2,7)
- B:(13,-7)
- C:(2,-7)
- D:(13,,13)
答 案:B
解 析:根据a=(3,1),b=(-2,5),则3a-2b=3×(3,1)-2×(-2,5)=(13,-7)
3、设 成等比数列,则x等于
成等比数列,则x等于
- A:0或-2
- B:1或-1
- C:0或-2
- D:-2
答 案:C
解 析:由已知条件的得
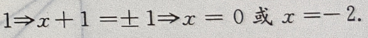
4、已知函数f(x)=5x+b,若f(-2)=3,则b=()。
- A:3
- B:15
- C:7
- D:13
答 案:D
主观题
1、已知log53=a,log54=b,求log2512关于a,b的表达式。
答 案:
2、在△ABC中,已知三边 a、b、c 成等差数列,且最大角∠A是最小角的2倍, a: b :c.
答 案: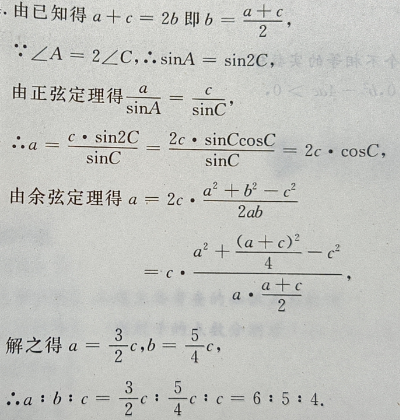
3、已知函数ƒ(x)=ax3-x2+bx+1(a,b∈R)在区间(-∞,0)和(1,+∞)上都是增函数,在(0,1)内是减函数. (Ⅰ)求a,b的值; (Ⅱ)求曲线y=ƒ(x)在x=3处的切线方程.
答 案:(Ⅰ)因为函数ƒ(x)在(-∞,0)上递增,在(0,1)内递减,在(1,+∞)上有递增,可知函数在x=0和x=1处的导数值均为0. 又f’(x)=3ax2-2x+b,
所以f’(0)=b=0,f’(1)=3a-2+b=0. 即切点为(3.10),所以其切线方程为y-10=12(x-3),即12x-y-26 = 0.
即切点为(3.10),所以其切线方程为y-10=12(x-3),即12x-y-26 = 0.
解 析:【考点指要】本题主要考查函数导数的几何意义、导数的求法和导数的应用——函数的单调区间及曲线的切线方程的求法
4、设椭圆的中心是坐标原点,长袖在x轴上,离心率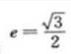 ,已知点P(0,3/2)到椭圆上的点的最远距离是
,已知点P(0,3/2)到椭圆上的点的最远距离是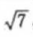 ,求椭圆的方程。
,求椭圆的方程。
答 案:
填空题
1、不等式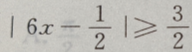 的解集是()
的解集是()
答 案: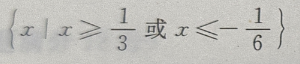
解 析: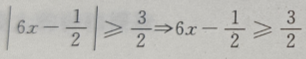 或
或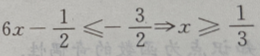 或
或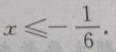
2、已知10x=3,10y=4,则103(x-y)的值等于______。
答 案: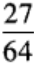
解 析:由已知,103x=27,103y=64,原式=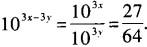
精彩评论