2025年成考高起点每日一练《数学(理)》5月14日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、过抛物线x2=-8y的焦点且倾斜角为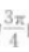 的直线方程是()。
的直线方程是()。
- A:x+y+2=0
- B:x-y+2=0
- C:x+y-2=0
- D:x-y-2=0
答 案:A
解 析:抛物线x2=-8y的焦点为F(0,-2),直线斜率为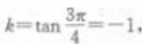 所求直线方程是 y+2=-(x-0),即x+y+2=0.(答案为A)
所求直线方程是 y+2=-(x-0),即x+y+2=0.(答案为A)
2、如果球的大圆面积增为原来的4倍,则该球的体积就增为原来的()。
- A:4倍
- B:8倍
- C:12倍
- D:16倍
答 案:B
解 析:
3、设集合M={1,2,4},N={2,3,5},则集合M∪N=().
- A:{2}
- B:{1,2,3,4,5}
- C:{3,5}
- D:{1,4}
答 案:B
解 析:M∪N={1,2,4}∪{2,3,5)= {1,2,3,4,5} (答案为B)
4、设双曲线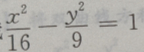 的渐近线的斜率为k,则|k|=()
的渐近线的斜率为k,则|k|=()
- A:
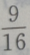
- B:
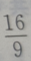
- C:
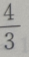
- D:
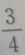
答 案:D
解 析:双曲线渐近线的斜率为k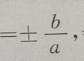 故本题中k
故本题中k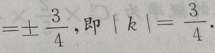
主观题
1、求函数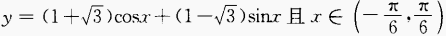 上的最大值以及取得这个最大值的x。
上的最大值以及取得这个最大值的x。
答 案:.1 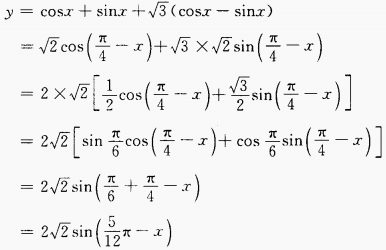
 函数取最大值,即y最大值=。
函数取最大值,即y最大值=。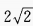
2、设a为实数,且tanα和tanβ是方程ax2+(2a-3)x+(a-2)=0的两个实根,求tan(α+β)的最小值。
答 案:由已知得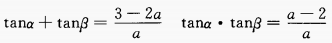

3、化简: (1)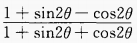
(2)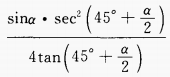
答 案:(1) (2)
(2)
4、(1)已知tanα=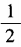 ,求cot2α的值; (2)已知tan2α=1,求tanα的值。
,求cot2α的值; (2)已知tan2α=1,求tanα的值。
答 案:(1)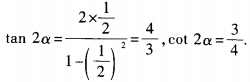 (2)由已知,得
(2)由已知,得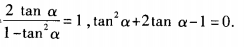 解关于tanα的一元二次方程,得tanα=
解关于tanα的一元二次方程,得tanα=
填空题
1、一个问题在1小时内,甲能独立解决的概率是0.5,乙能独立解决的概率是0.4,两人在1小时内解决问题的概率是______。
答 案:0.7
解 析:设事件A为两人在1小时内解决问题,即1小时内至少有一人能解决问题,事件B为甲在1小时内解决问题,事件C为乙在1小时内解决问题,事件B、C是相互独立事件,事件A的对立事件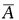 互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(
互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(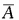 )=1-P(
)=1-P(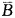 ·
·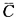 )=1-P(
)=1-P(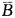 )·P(
)·P(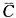 )
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
)
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
2、y=cos22x的最大值是______,最小值______,周期T=______。
答 案:1;0;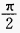
解 析: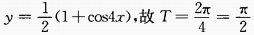 ,最大值为
,最大值为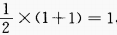 ,最小值为
,最小值为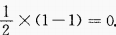
精彩评论