2025年成考高起点每日一练《数学(理)》5月18日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、下列四个命题中正确的是（）。 ①已知a，b，c三条直线，其中a，b异面，a//c，则b，c异面。
②若a与b异面，b与c异面，则a与c异面。
③过平面外一点与平面内一点的直线，和平面内不经过该点的直线是异面直线。
④不同在任何一个平面内的两条直线叫异面直线。

• A：③④
• B：②③④
• C：①②③④
• D：①②

答 案：A

解 析：①b与c可相交，②a与c可以有平行、相交、异面三种位置关系。答案为A。  

2、函数f(x)=x³-6x²+9x-3的单调区间为（）。

• A：(-∞，-3)、(-3，1)、(1，+∞)
• B：(-∞，-1)、(-1，3)、(3，+∞)
• C：(-∞，1)、(1，3)、(3，+∞)
• D：(-∞，-3)、(-3，-1)、(-1，+∞)

答 案：C

解 析：y=x³-6x²+9x-3则y’=3x²+12x+9 令y’=0,x²-4x+3=0（x-1）（x-3）=0解得，x1=1，x2=3 四个答案中，只有C具有1、3两个极值点，其余3个没有，故应选C。  

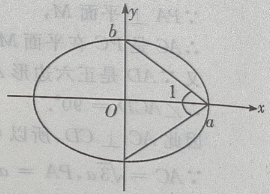
3、从椭圆与x轴额右交点看短轴两端点的视角为60°的椭圆的离心率（）  

• A：
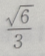
• B：
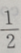
• C：1
• D：

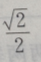
答 案：A

解 析：求椭圆的离心率,先求出a,c.(如图) 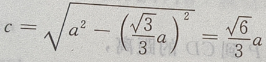，由椭圆定义知

4、如果不共线的向量a和b有相等的长度,则(a+b)(a-b)=（）  

• A：0
• B：1
• C：-1
• D：2

答 案：A

解 析：(a+b)(a-b)=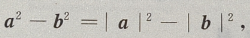

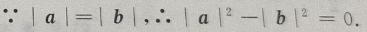
主观题

1、设a为实数，且tanα和tanβ是方程ax²+（2a-3）x+（a-2）=0的两个实根，求tan（α+β）的最小值。

答 案：由已知得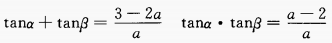

2、已知log₅3=a，log₅4=b，求log₂₅12关于a，b的表达式。  

答 案：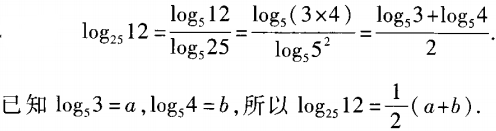

3、求下列函数的定义域： （1）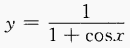
（2）
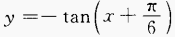
（3）  

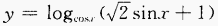
答 案：（1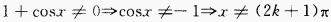） ∴函数的定义域为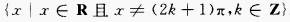（2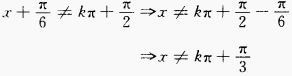） ∴函数的定义域为（3）
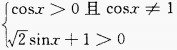
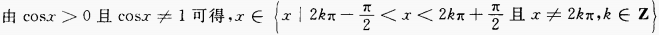
由对数函数的性质知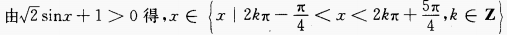， 故函数的定义域为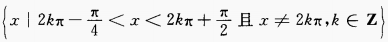  

4、试证明下列各题
（1）
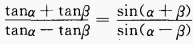
（2）

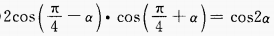
答 案：（1）化正切为正、余弦，通分即可得证。 （2）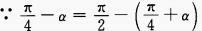

填空题

1、九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。  

答 案：85  

解 析：本题主要考查的知识点为中位数. 将成绩按由小到大排列：63，77，79，81，85，88，89，94，99.因此中位数为85。

2、lg(tan43°tan45°tan47°)=（）  

答 案：0

解 析：lg(tan43°tan45°tan47°)=lg(tan43°tan45°cot43°)=lgtan45°=lg1=0