2025年成考高起点每日一练《数学(理)》5月19日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、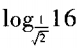 =()。
=()。
- A:8
- B:-8
- C:2
- D:-2
答 案:B
解 析:由于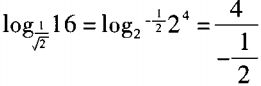 。log22=-8。故选B。
。log22=-8。故选B。
2、已知3sin2α+8sinα-3=0,则cos2α=()。
- A:
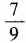
- B:
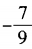
- C:
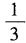
- D:
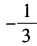
答 案:A
解 析:由已知得(3sinα-1)(sinα+3)=0。 由于|sinα|≤1,所以sinα=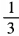 。因此
。因此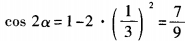 。故选A。
。故选A。
3、已知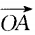 =(3,2),
=(3,2),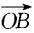 =(-4,y),并其人
=(-4,y),并其人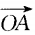 ⊥
⊥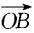 ,则
,则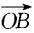 的长度为()。
的长度为()。
- A:
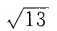
- B:
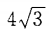
- C:
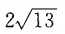
- D:
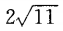
答 案:C
解 析: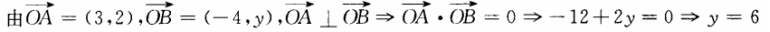
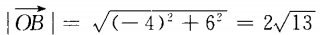
4、函数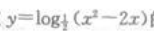 的定义域是()。
的定义域是()。
- A:(-∞,0)∪[2,+∞)
- B:[0,2]
- C:(-∞,0)∪(2,+∞)
- D:(0,2)
答 案:C
解 析:x2-2x>0,解得x<0或x>2.函数的定义域为(-∞,0)∪(2,+∞)。答案为C。
主观题
1、在△ABC中如果sinA=2sinBcosC,求证:△ABC是等腰三角形。
答 案: ∴△ABC为等腰三角形。
∴△ABC为等腰三角形。
2、设 分别讨论x→0及x→1时f(x)的极限是否存在?
分别讨论x→0及x→1时f(x)的极限是否存在?
答 案: ∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
3、求将抛物线y=x2-2x-3平移到顶点与坐标原点重合时的函数解析式。
答 案:
4、设a为实数,且tanα和tanβ是方程ax2+(2a-3)x+(a-2)=0的两个实根,求tan(α+β)的最小值。
答 案:由已知得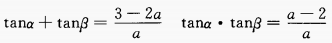

填空题
1、sin210°+sin220°+sin240°+sin250°+sin270°+sin280=______。
答 案:3
解 析:由互为余角的余函数值相等得 原式=(sin210°+cos210°)+(sin220°+cos220°)+(sin240+cos240)=1+1+1=3
2、过点(2,0)作圆x2+y2=1的切线,切点的横坐标为()。
答 案: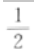
解 析:本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有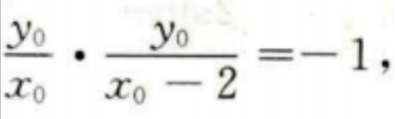 即
即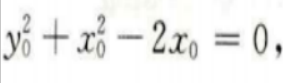
 所以
所以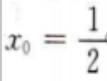 故切点横坐标为
故切点横坐标为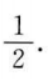
精彩评论