2025年成考高起点每日一练《数学(理)》5月22日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知偶函数y=f(x),在区间[a,b](0 答 案:B 解 析:由偶函数的性质:偶函数在[a,b]和[-b,-a]上有相反的单调性,可知,y=f(x)在区间[a,b](0 2、已知 答 案:D 解 析: 3、已知圆的方程为x2+y2-2x+4y+1=0,则圆上一点到直线3x+4y-10=0的最大距离为()。 答 案:B 解 析:圆x2+y2-2x+4y+1=0,即(x-1)2+(y+2)2=22的圆心为(1,-2)半径r=2,
圆心(1.-2)到直线3x+4y-10=0的距离是 4、两条直线是异面直线的充分条件是这两条直线()。 答 案:D 主观题 1、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35° 2、求将抛物线y=x2-2x-3平移到顶点与坐标原点重合时的函数解析式。
答 案: 3、已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。 答 案:由已知,得 4、(1)已知tanα= 答 案:(1) 填空题 1、函数 答 案:-1 解 析: 2、 答 案: 解 析:当sin2x=-1时,y最小值 ,则sin2α=()
,则sin2α=()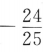
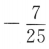
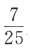
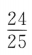
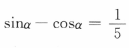 两边平方得
两边平方得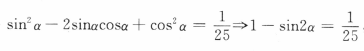 ,故
,故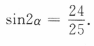
 圆上一点到直线3x+4y-10=0的距离的最大值是3+2=5.(答案为B)
圆上一点到直线3x+4y-10=0的距离的最大值是3+2=5.(答案为B)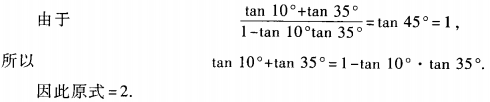

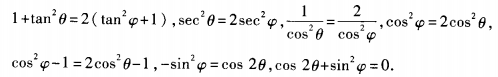
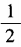 ,求cot2α的值; (2)已知tan2α=1,求tanα的值。
,求cot2α的值; (2)已知tan2α=1,求tanα的值。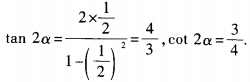 (2)由已知,得
(2)由已知,得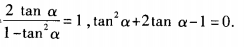 解关于tanα的一元二次方程,得tanα=
解关于tanα的一元二次方程,得tanα=
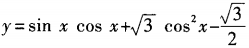 (x∈R)的最小值为______。
(x∈R)的最小值为______。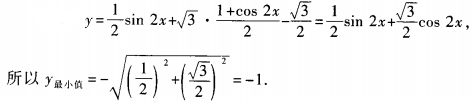
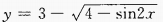 的值域是______。
的值域是______。
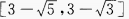
 当 sin2x=1时,
当 sin2x=1时,
精彩评论