2025年成考高起点每日一练《数学(文史)》5月22日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、某车间有甲、乙两台机床，已知甲机床停机的概率为0.06，乙机床停机的概率为0.07，甲、乙两车床同时停机的概率是（）。

• A：0.13
• B：0.0042
• C：0.03
• D：0.04

答 案：B

2、（）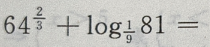  

• A：8
• B：14
• C：12
• D：10

答 案：B

解 析：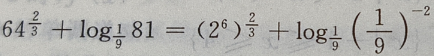

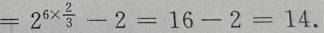
3、函数f(x)=当x∈[-2,+∞)时是增函数，当x∈(-∞,-2]时是减函数，则f(1)=()  

• A：-3
• B：13
• C：7
• D：由m而定的常数

答 案：B

解 析：由题意知抛物线的对称轴为x=-2，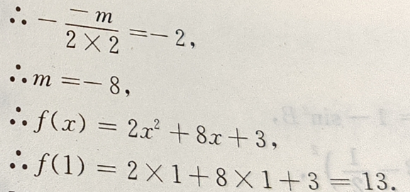  

4、若log₁₅5=m，则log₁₅3=（）。

• A：
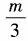
• B：1+m
• C：1-m
• D：m-1

答 案：C

解 析：log₁₅3=log₁₅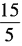=log₁₅15-log₁₅5=1-m选C。

主观题

1、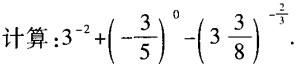  

答 案：

2、已知等差数列前n项和 （Ⅰ）求通项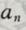的表达式 （Ⅱ）求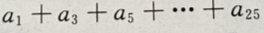的值  

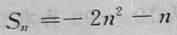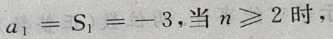
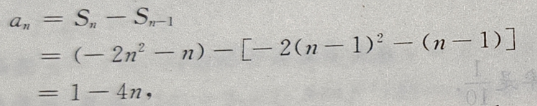
答 案：（Ⅰ）当n=1时，由得 也满足上式，故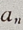=1-4n（n≥1） （Ⅱ）由于数列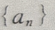是首项为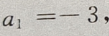公差为d=-4的等差数列，所以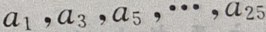是首项为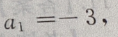公差为d=-8，项数为13的等差数列，于是由等差数列前n项和公式得：  

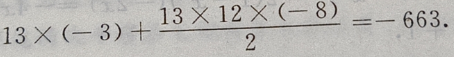
3、设椭圆的中心是坐标原点,长轴在x轴上,离心率已知点P到圆上的点的最远距离是求椭圆的方程  

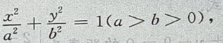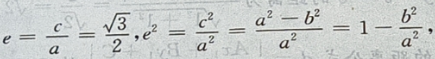
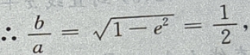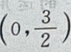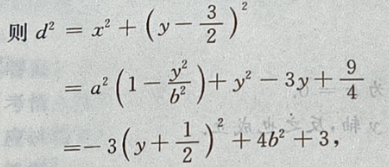
答 案：由题意，设椭圆方程为 由 设P点到椭圆上任一点的距离为 d, 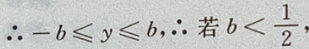则在y=-b时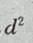，最大，即d也最大。  

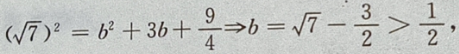
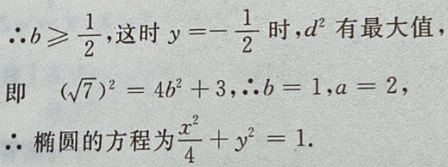
4、教室里有50人在开会，其中学生35人，家长12人，老师3人，现校长在门外听到有人在发言，那么发言人是老师或学生的概率为多少？  

答 案：此题属于互斥事件，发言人是老师的概率为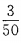，是学生的概率为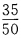，故所求概率为。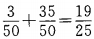

填空题

1、化简sin（x+y）-2cosxsiny=______。  

答 案：sin（x-y）

解 析：原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin（x-y）  

2、函数y=2x(x+1)在x=2处的切线方程是__________．  

答 案：10x-y-8=0

解 析：由函数y=2x(x+1) 知，y´=(2x2+2x)'=4x+2，则y´|x=2=10．又当x=2时，y=12，知此函数的切线过点(2，12)，且斜率为10。则其切线方程为10(x-2)=y-12，即10x-y-8=0． 【考点指要】本题考查利用导数求曲线的切线方程，y=ƒ(x)在点P(x0，y0)处的导数值即为曲线y=ƒ(x)在该点处切线的斜率．