2025年成考高起点每日一练《数学(理)》5月24日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

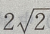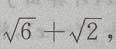
1、在△ABC中，若b=，c=则a等于（）

• A：2
• B：
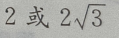
• C：
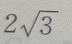
• D：无解

答 案：B

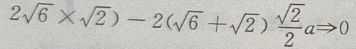
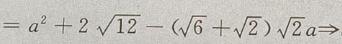
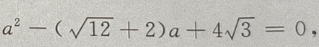解 析：此题是已知两边和其中一边的对角,解三角形时,会出现一解、两解、无解的情况,要注意这一点.用余弦定理可得解出

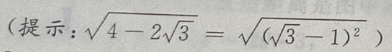
2、在△ABC中，∠C=90°，∠B=30°，D是BC上的一点，∠ADB=135°，AC=2，则BD等于（）。  

• A：
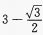
• B：
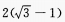
• C：
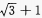
• D：

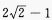
答 案：B

解 析：由已知得，AC=CD=2，设BD=x，在Rt△ABC中，BC=2cot30°=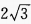  

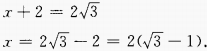
3、设集合M={x∈R|x2=1}，N={x∈R|x3=1}，则M∩N=（）。

• A：{1}
• B：{-1}
• C：{-1，1}
• D：

答 案：A

解 析：本题主要考查的知识点为集合的运算 由题意M={-1，1}，N={1}，所以M∩N={1}

4、已知点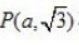在曲线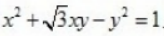上，那么a的值是（）。

• A：1
• B：1或-4
• C：-4或-1
• D：-4

答 案：B

主观题

1、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得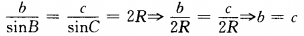

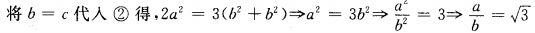
∴a：b=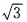：1
于是a：b：c=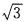：1：1。  

2、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得AB=120m,求河的宽

答 案：如图， ∵∠C=180°-30°-75°=75° ∴△ABC为等腰三角形，则AC=AB=120m 过C做CD⊥AB,则由Rt△ACD可求得CD==60m， 即河宽为60m  

3、设a为实数，且tanα和tanβ是方程ax²+（2a-3）x+（a-2）=0的两个实根，求tan（α+β）的最小值。

答 案：由已知得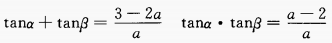

4、已知函数f(x)=(x-4)(x²-a) （I）求f"(x)； (Ⅱ)若f"(-1)=8，求f(x)在区间[0，4]的最大值与最小值

答 案：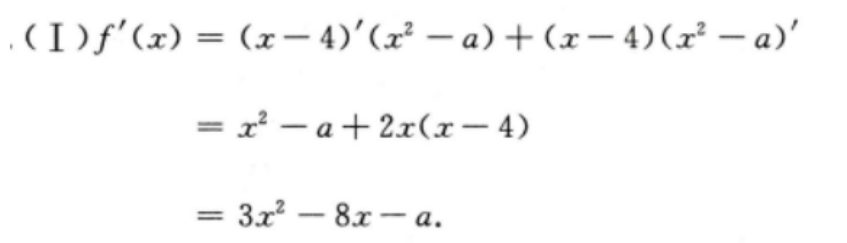

填空题

1、从甲、乙、丙3名学生中随机选2人，则甲被选中的概率为          .

答 案：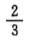

解 析：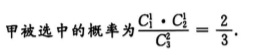

2、若tanα-cotα=1，则=______。

答 案：4

解 析：由立方差公式得,tan³α-cot³α=(tana-cotα)(tan²α+tanαcota+cot²α)(tana-cotα)[(tanα-cotα)²+3tanαcotα]=4