2025年成考高起点每日一练《数学(文史)》5月24日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、b=0是直线y=kx+b过原点的（）

• A：充分但不必要条件
• B：必要但不充分条件
• C：充要条件
• D：既不充分也不必要条件

答 案：C

解 析：b=0直线y=kx+b过原点

2、设集合M={1，2，3，4，5}，N={2，4，6}，T={4，5，6}则（M∩T）∪N是（）。  

• A：{2，4，5，6}
• B：{4，5，6}
• C：{1，2，3，4，5，6}
• D：{2，4，6}

答 案：A

3、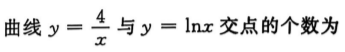

• A：3
• B：2
• C：1
• D：0

答 案：C

解 析：由反比例函数和对数函数的图像可知，两个函数仅在第一象限有一个交点.

4、盒中有20节电池，其中有2节是废品，现从中取3节，其中至少有一节废品的概率是（）。

• A：
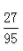
• B：
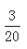
• C：
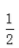
• D：

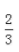
答 案：A

主观题

1、如图9-4，已知测速站P到公路L的距离为40米，一辆汽车在公路L上行驶，测得此车从A点行驶到8点所用的时间为2秒，并测得∠APO=60°，∠BPO=30°，计算此车从A到B的平均速度为多少km/h（结果保留到个位），并判断此车是否超过了80km/h的限制速度。

答 案：此车从A到B的平均速度为83（km/h），已经超过80km/h的限制速度。

2、已知a-a^-1=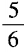，求a³-a^-3的值。  

答 案：

3、若tanα、tanβ是关于x的方程mx²-(2m-3)x+m-2=0的两个实根，求tan(α+β)的取值范围

答 案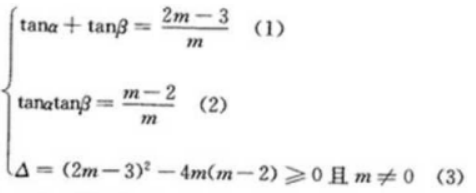： 由(1)(2)得，tan(a+β)=m-3/2;由(3)得m≤9/4且m≠0所以tan(a+β)的取值范围是(-∞，-3/2)U(-3/2，3/4)  

4、求函数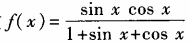（x∈R）的最大值与最小值。  

答 案：设sinx+cosx=t，则（sinx+cosx）²=t²，1+2sinxcosx=t²，sinxcosx= 于是转化为求的最值。 由所设知 上为增函数，故g（t）的最大值为最小值为

填空题

1、九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。  

答 案：85  

解 析：本题主要考查的知识点为中位数. 将成绩按由小到大排列：63，77，79，81，85，88，89，94，99.因此中位数为85。

2、全集U，集合M，N如图1—7所示，用列举法表示M，N，CUM，CUN。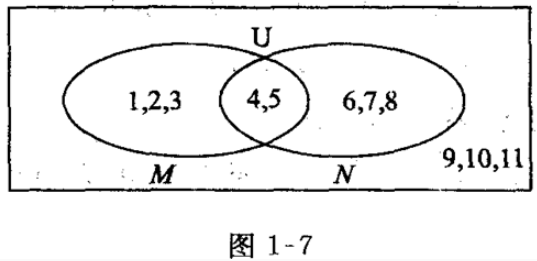

答 案：如图1—7，有M={1，2，3，4，5}，N={4，5，6，7，8}，CUM={6，7，8，9，10，11}，CUN=｛1，2，3，9，10，11｝。