2025年成考专升本每日一练《高等数学一》3月13日专为备考2025年高等数学一考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设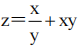，则（）  

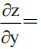• A：
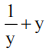
• B：
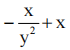
• C：
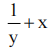
• D：

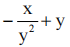
答 案：B

解 析：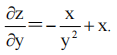

2、方程x＝z²表示的二次曲面是（）。

• A：球面
• B：椭圆抛物面
• C：柱面
• D：圆锥面

答 案：C

解 析：方程x＝z²是以xOy坐标面上的抛物线x＝z²为准线，平行于y轴的直线为母线的抛物柱面。

3、当x→2时，下列变量中为无穷小量的是（）。

• A：
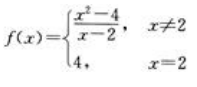
• B：f（x）＝（2－x）×2
• C：
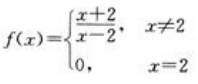
• D：

答 案：B

解 析：A项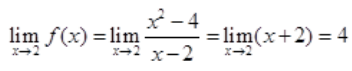，；B项，；CD两项，。

主观题

1、设D是由直线y＝x与曲线y＝x³在第一象限所围成的图形.（1）求D的面积S；
（2）求D绕x轴旋转一周所得旋转体的体积V。

答 案：解：由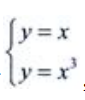，知两曲线的交点为（0，0），（1，1）和（-1，-1），则（1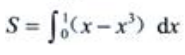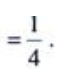）（2）

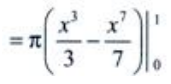
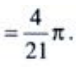
2、求。

答 案：解：。

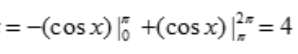3、设有一圆形薄片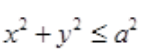，在其上一点M（x，y）的面密度与点M到点（0，0）的距离成正比，求分布在此薄片上的物质的质量。

答 案：解：设密度为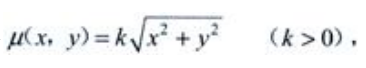故质量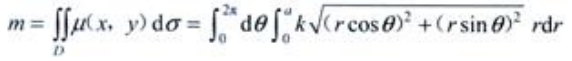

填空题

1、设f（x，y）＝x＋y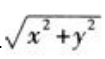－，则f′x（3，4）＝（）。

答 案：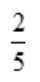

解 析：，

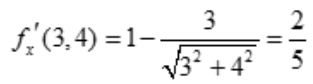
2、＝（）。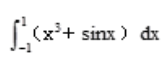

答 案：

解 析：被积函数x³＋sinx为奇函数，且积分区域关于原点对称，由定积分的对称性得＝0。

3、设y=2^x+sin2，则y’=（）。  

答 案：2^xln2。

解 析：本题考查的知识点为初等函数的求导运算。本题需利用导数的四则运算法则求解。  

简答题

1、  

答 案：积分区域D如图2-1所示。 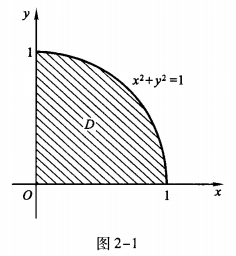解法1利用极坐标系。

解 析：本题考查的知识点为计算二重积分；选择积分次序或利用极坐标计算。