2025年成考专升本每日一练《高等数学一》3月17日专为备考2025年高等数学一考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设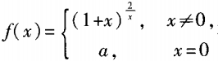在点x=0处连续。则α=（）。  

• A：1
• B：2
• C：e
• D：e²

答 案：D

解 析：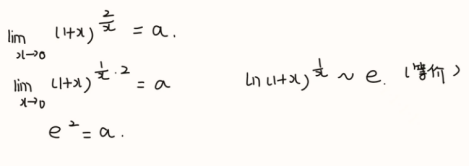

2、函数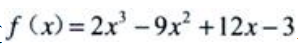单调减少的区间为（）。

• A：（－∞，1]
• B：[1，2]
• C：[2，＋∞）
• D：[1，＋∞）

答 案：B

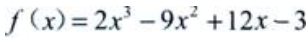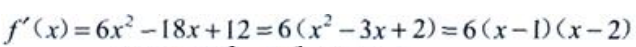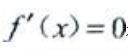解 析：的定义域为（－∞，＋∞），求导得令得驻点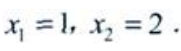当x＜1时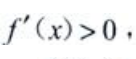，f（x）单调增加；当1＜x＜2时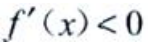，，f（x）单调减少；当x＞2时，f（x）单调增加.故单调递减区间为[1，2]。

3、过点（1，0，0），（0，1，0），（0，0，1）的平面方程为（）。  

• A：x+y+z=1
• B：2x+y+z=1
• C：x+2y+z=1
• D：x+y+2z=1

答 案：A

解 析：设所求平面方程为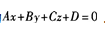。由于点（1，0，0），（0，1，0），（0，0，1）都在平面上，将它们的坐标分别代入所设平面方程，可得方程组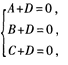 故选A。

主观题

1、在曲线上求一点M₀，使得如图中阴影部分的面积S₁与S₂之和S最小。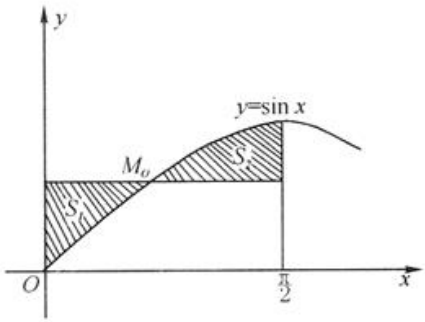

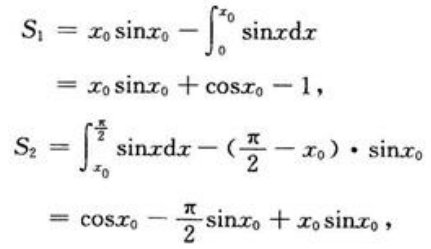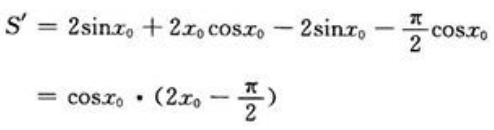答 案：解：设点M₀的横坐标为x₀，则有则S为x₀的函数，将上式对x₀求导得令S'=0,得，所以由于只有唯一的驻点，所以则点M₀的坐标为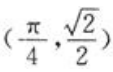为所求。

2、计算．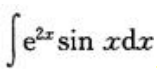

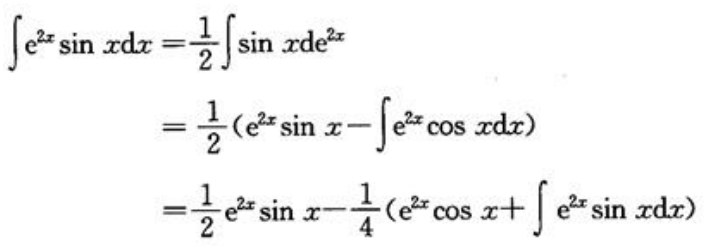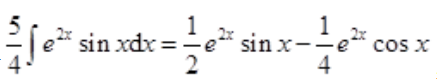答 案：解：从而有，所以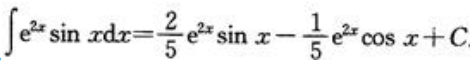

3、设函数f（x）＝x-lnx，求f（x）的单调增区间．

答 案：解：函数f（x）的定义域为（0，＋∞）。令y＝f（x），则令y'＝0，解得x＝1。当0＜x＜1时，y'＜0；当x＞1时，y'＞0。
因此函数f（x）的单调增区间为（1，＋∞）。

填空题

1、设y＝x²e^x，则y'＝（）。

答 案：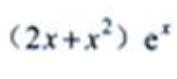

解 析：由函数乘积的导数公式，可得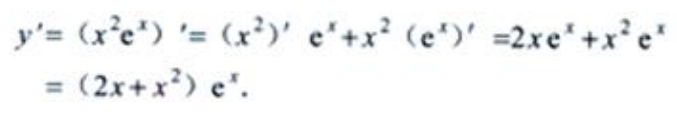

2、级数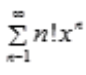的收敛半径是（）。

答 案：

解 析：

3、二阶常系数齐次微分方程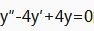的通解为_____。  

答 案：

解 析：  

简答题

1、求曲线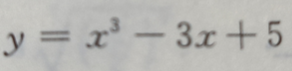的拐点；  

答 案：