2025年成考专升本每日一练《高等数学二》3月21日专为备考2025年高等数学二考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、若，则。（）  

答 案：错

解 析：

单选题

1、设函数z＝x³＋y³，则（）.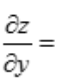

• A：3x²
• B：3x²＋3y²
• C：
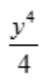
• D：3y²

答 案：D

解 析：求z对y的偏导，将x看作常数，故.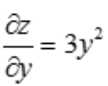

2、（）。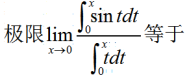  

• A：-1
• B：0
• C：1
• D：2

答 案：C

主观题

1、计算

答 案：解：

2、设曲线y＝cosx（0≤x≤π/2）与x轴、y轴所围成的图形面积被曲线y＝asinx，y＝bsinx（a＞b＞0）三等分，试确定a、b的值．

答 案：解：由y＝cosx，y＝asinx，得tanx＝1/a，故有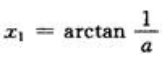；同理可求得.因为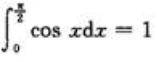，令这三部分的面积分别为D₁，D₂，D₃，有D₁＝D₂＝D₃＝1/3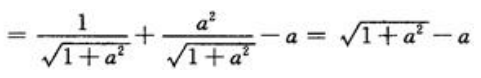．，故a＝4/3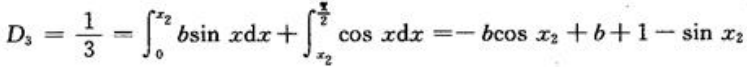．故b＝5/12．

填空题

1、若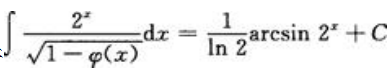，则＝()．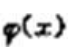

答 案：4^x

解 析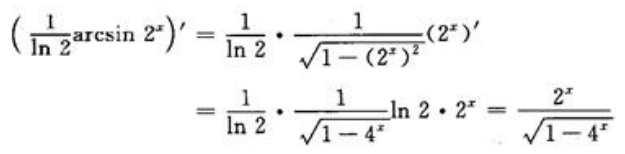：根据不定积分定义可知，有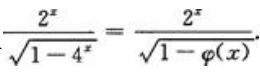故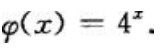

2、（）．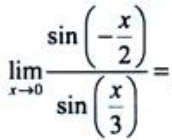

答 案：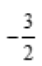

解 析：由等价无穷小知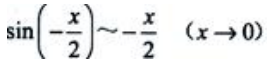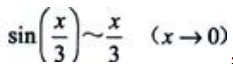，，所以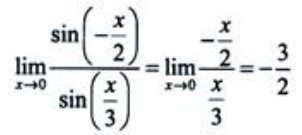

简答题

1、设z=x（x，y）由方程e^z-xy²+sin（y+z）=0确定，求Dz。  

答 案：本题考查的知识点是二元隐函数全微分的求法。

 

2、甲、乙二人单独译出某密码的概率分别为0.6和0.8，求此密码被破译的概率。  

答 案：本题考查的知识点是事件相互独立的概念和概率的加法公式。