2025年成考专升本每日一练《高等数学一》4月7日专为备考2025年高等数学一考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、曲线y=-ex在点(0,-1)处切线的斜率k=()。
- A:2
- B:1
- C:0
- D:-1
答 案:C
解 析:切线的斜率即为函数在该点的导数值 ,则
,则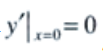 。
。
2、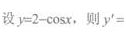 ()。
()。
- A:1-sinx
- B:1+sinx
- C:-sinx
- D:sinx
答 案:D
解 析:
3、设函数f(x)满足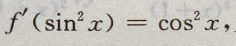 且f(0)=0,则f(x)=()
且f(0)=0,则f(x)=()
- A:

- B:
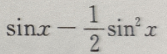
- C:
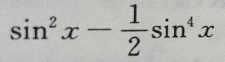
- D:
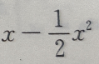
答 案:D
解 析:由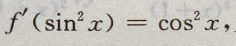 知
知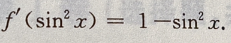 令
令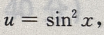 故
故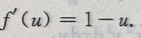 所以f(u)=u-
所以f(u)=u-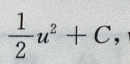 由f(0)=0,得C=0.所以
由f(0)=0,得C=0.所以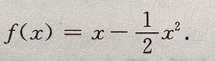
主观题
1、将函数f(x)=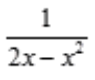 展开为x-1的幂级数,并指出收敛区间(不讨论端点)。
展开为x-1的幂级数,并指出收敛区间(不讨论端点)。
答 案:解: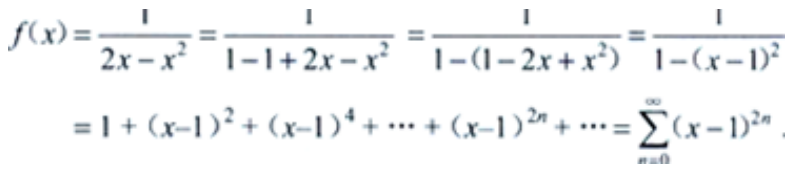 由
由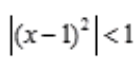 ,知-1<x-1<1,0<x<2,即收敛区间是(0,2)。
,知-1<x-1<1,0<x<2,即收敛区间是(0,2)。
2、试证:当x>0时,有不等式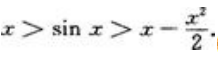
答 案:证:先证x>sinx(x>0)。设f(x)=x-sinx,则f(x)=1-cosx≥0(x>0),所以f(x)为单调递增函数,于是对x>0有f(x)>f(0)=0,即x-sinx>0,亦即x>sinx(x>0)。再证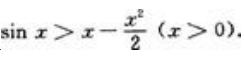
令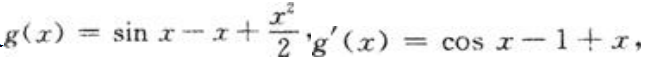
则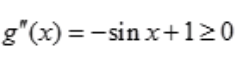 ,所以g'(x)单调递增,又g'(x)=0,可知g'(x)>g'(0)=0(x>0),那么有g(x)单调递增,又g(0)=0,可知g(x)>g(0)=0(x>0),所以
,所以g'(x)单调递增,又g'(x)=0,可知g'(x)>g'(0)=0(x>0),那么有g(x)单调递增,又g(0)=0,可知g(x)>g(0)=0(x>0),所以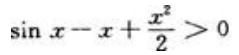 即
即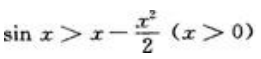
综上可得:当x>0时,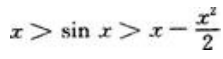 。
。
3、求微分方程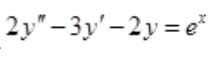 的通解。
的通解。
答 案:解: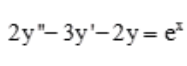 的特征值方程为
的特征值方程为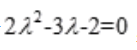 ,则
,则 ;故齐次微分方程的通解为
;故齐次微分方程的通解为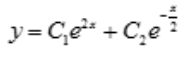 。由题意设原微分方程的特解为
。由题意设原微分方程的特解为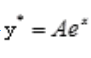 ,则有
,则有 ,得
,得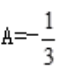 。即微分方程的通解为
。即微分方程的通解为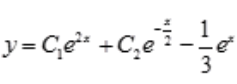 。
。
填空题
1、设D为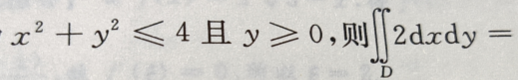 ()
()
答 案:
解 析:因积分区域为圆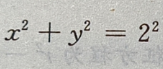 的上半圆,则
的上半圆,则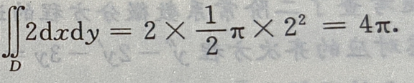
2、设 则y'=()。
则y'=()。
答 案: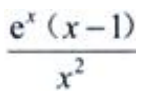
解 析:
3、设区域D由y轴,y=x,y=1所围成,则
答 案: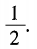
解 析:本题考查的知识点为计算二重积分。其积分区域如图1-1阴影区域所示: 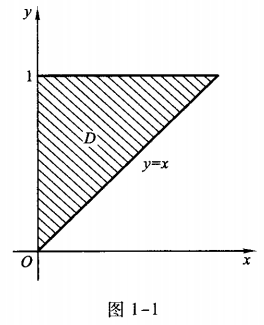
可利用二重积分的几何意义或将二重积分化为二次积分解之。
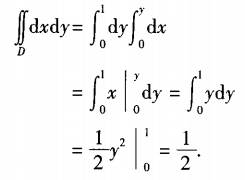
简答题
1、
答 案:
精彩评论