2025年成考专升本每日一练《高等数学二》4月9日专为备考2025年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析:
单选题
1、A、B、C、D、E五人并排站成一排,如果B必须站在A的右边且A,B不可相邻,那么不同的排法有()。
- A:24种
- B:36种
- C:90种
- D:120种
答 案:B
2、在x趋向于()时, 为无穷小量.
为无穷小量.
- A:2
- B:1
- C:-1
- D:+∞
答 案:D
解 析:A项,当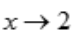 时,
时,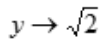 ;B项,当
;B项,当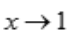 时,
时,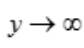 ;C项,由题意x≥0,且x≠1,故x不能趋向于-1;D项,当
;C项,由题意x≥0,且x≠1,故x不能趋向于-1;D项,当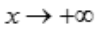 时,因为分子x的次幂小于分母中x的次幂,故
时,因为分子x的次幂小于分母中x的次幂,故 ,即为无穷小.
,即为无穷小.
主观题
1、己知离散型随机变量X的概率分布为 (1)求常数a;
(1)求常数a;
(2)求X的数学期望EX.
答 案:解:(1)因为0.2+0.1+0.5+a=1,所以a=0.2.(2)EX=10×0.2+20×0.1+30×0.5+40×0.2=27.
2、设函数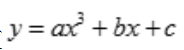 ,在点x=1处取得极小值-1,且点(0,1)是该曲线的拐点,试求常数a,b,c及该曲线的凹凸区间.
,在点x=1处取得极小值-1,且点(0,1)是该曲线的拐点,试求常数a,b,c及该曲线的凹凸区间.
答 案:解: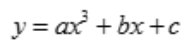 ,则
,则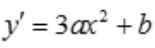 ,
,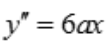 .由y(1)=-1,y(0)=1,y'(1)=0,得方程组
.由y(1)=-1,y(0)=1,y'(1)=0,得方程组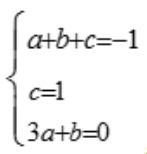 ,解得a=1,b=-3,c=1,所以
,解得a=1,b=-3,c=1,所以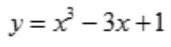 ,当x>0时,y''>0,则曲线的凹区间为(0,+∞);当x<0时,y''<0,则曲线
,当x>0时,y''>0,则曲线的凹区间为(0,+∞);当x<0时,y''<0,则曲线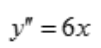 的凸区间为(-∞,0).
的凸区间为(-∞,0).
填空题
1、 ()
()
答 案:
解 析: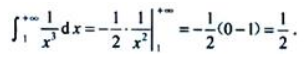
2、若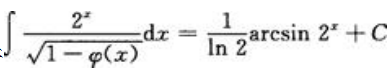 ,则
,则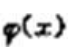 =().
=().
答 案:4x
解 析: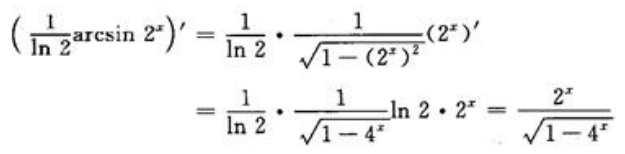 根据不定积分定义可知,有
根据不定积分定义可知,有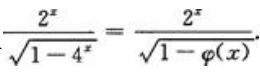 故
故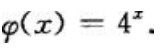
简答题
1、求函数ƒ(x)=x3-3x+1的单调区间和极值。
答 案:函数的定义域为(-∞,+∞),且ƒ'(x)=3x2-3,令ƒ'(x)=0,得驻点x=-1,x2=1。列表如下:  由上表可知,函数ƒ(x)的单调增区间为(-∞,-1]和[1,+∞),单调减区间为[-1,1];ƒ(-1)=3为极大值ƒ=-1为极小值。
由上表可知,函数ƒ(x)的单调增区间为(-∞,-1]和[1,+∞),单调减区间为[-1,1];ƒ(-1)=3为极大值ƒ=-1为极小值。
解 析:注意:如果将(-∞,-1]写成(-∞,-1),[1,+∞)写成(1,+∞),[-1,1]写成(-1,1)也正确。
2、设随机变量X的概率分布为: 求X的期望、方差以及标准差.
求X的期望、方差以及标准差.
答 案: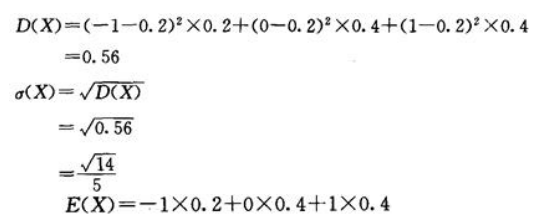
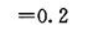
精彩评论