2025年成考专升本每日一练《高等数学一》4月24日专为备考2025年高等数学一考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、直线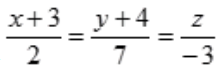 与平面4x-2y-3z-3=0的位置关系是()。
与平面4x-2y-3z-3=0的位置关系是()。
- A:直线垂直平面
- B:直线平行平面但不在平面内
- C:直线与平面斜交
- D:直线在平面内
答 案:C
解 析:直线的方向向量s=(2,7,-3),且此直线过点(-3,-4,0),已知平面的法向量n=(4,-2,-3),故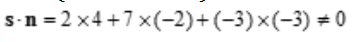 ,又因点(-3,-4,0)不在已知平面内,所以已知直线相交于已知平面。
,又因点(-3,-4,0)不在已知平面内,所以已知直线相交于已知平面。
2、y=cosx,则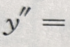 ()
()
- A:sinx
- B:cosx
- C:-cosx
- D:-sinx
答 案:C
解 析: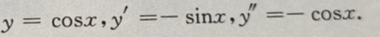
3、微分方程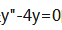 的特征根为()。
的特征根为()。
- A:0,4
- B:-2,2
- C:-2,4
- D:2,4
答 案:B
解 析:由r2-4=0,r1=2,r2=-2,知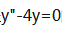 的特征根为2,-2,故选B。
的特征根为2,-2,故选B。
主观题
1、计算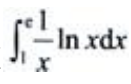 .
.
答 案:解:
2、计算二重积分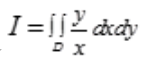 ,其中D是由
,其中D是由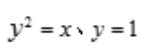 和x=4所围的平面区域(在第一象限)。
和x=4所围的平面区域(在第一象限)。
答 案:解:图形见下图中阴影部分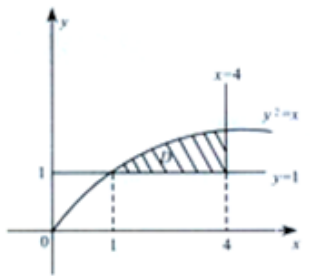 由y2=x得y=
由y2=x得y=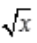 ,则
,则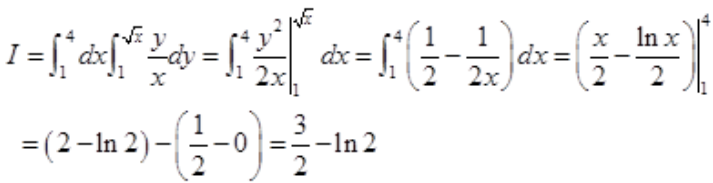
3、设f(x,y)为连续函数,交换二次积分 的积分次序。
的积分次序。
答 案:解:由题设知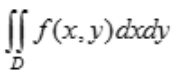 中积分区域的图形应满足1≤x≤e,0≤y≤lnx,因此积分区域的图形见下图中阴影部分
中积分区域的图形应满足1≤x≤e,0≤y≤lnx,因此积分区域的图形见下图中阴影部分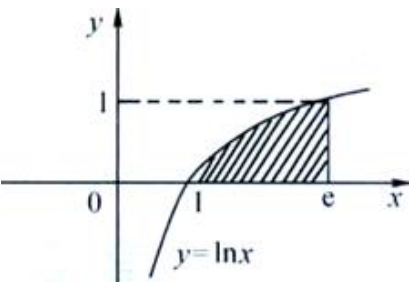 .由y=lnx,有x=ey。所以
.由y=lnx,有x=ey。所以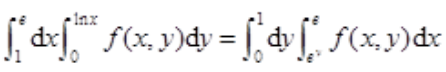 。
。
填空题
1、设函数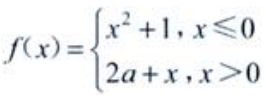 ,在x=0处连续,则a=()。
,在x=0处连续,则a=()。
答 案: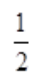
解 析:由于f(x)在点x=0处连续,故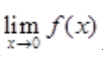 存在,且
存在,且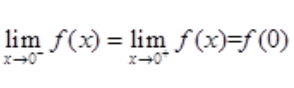 ,
,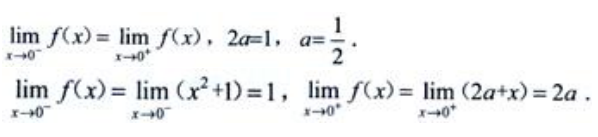
2、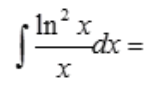 ()。
()。
答 案: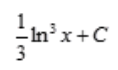
解 析: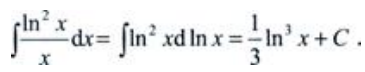
3、微分方程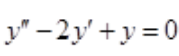 的通解是()。
的通解是()。
答 案:y=(C1+C2x)ex
解 析:微分方程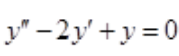 的特征值方程为
的特征值方程为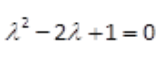 ,所以
,所以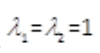 ,故其通解为
,故其通解为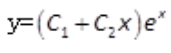 。
。
简答题
1、计算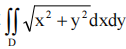 ,其中D是由曲线
,其中D是由曲线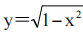 ,y=x,y=-x所围成的闭区域.
,y=x,y=-x所围成的闭区域.
答 案:积分区域用极坐标可表示为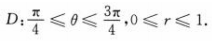 故
故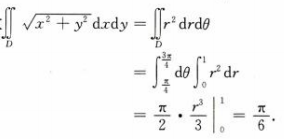
网友评论
共0条