2025年成考专升本每日一练《高等数学二》5月21日专为备考2025年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析:
单选题
1、设函数f(x)=cosx,则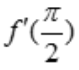 =().
=().
- A:-1
- B:
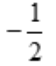
- C:0
- D:1
答 案:A
解 析: ,
,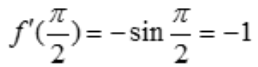 .
.
2、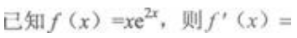 ()。
()。
- A:
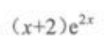
- B:
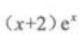
- C:
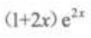
- D:

答 案:C
解 析: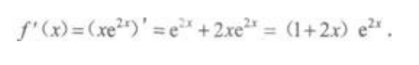
主观题
1、己知离散型随机变量X的概率分布为 (1)求常数a;
(1)求常数a;
(2)求X的数学期望EX.
答 案:解:(1)因为0.2+0.1+0.5+a=1,所以a=0.2.(2)EX=10×0.2+20×0.1+30×0.5+40×0.2=27.
2、某班有党员10人,其中女党员有6人,现选3人组成党支部.设事件A={党支部中至少有1名男党员},求P(A).
答 案:解: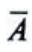 ={党支部中没有男党员},则
={党支部中没有男党员},则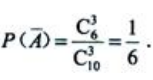 因为
因为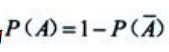 ,所以
,所以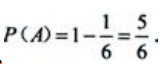
填空题
1、曲线y=x3+3x的拐点坐标为().
答 案:(0,0)
解 析: ,令y''=0,得x=0,y=0.当x<0时,y''<0;当x>0时,y''>0.故曲线的拐点为(0,0).
,令y''=0,得x=0,y=0.当x<0时,y''<0;当x>0时,y''>0.故曲线的拐点为(0,0).
2、设 则y'=()
则y'=()
答 案:
解 析: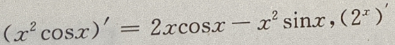
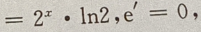 所以
所以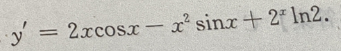
简答题
1、设离散型随机变量x的分布列为
①求常数a的值;
②求X的数学期望E(X)。
答 案:①随机变量的分布列必须满足规范性,所以0.2+a+0.5=1,得a=0.3.②E(X)=1×0.2+2×0.3+3×0.5=2.3
2、设函数y=ax3+bx+c在点x=1处取得极小值-1,且点(0,1)为该函数曲线的拐点,试求常数a,b,c。
答 案:本题考查的知识点是可导函数在某一点取得极小值的必要条件以及拐点的概念。 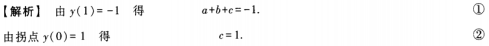
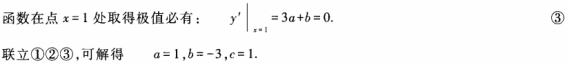
精彩评论