2025年成考专升本每日一练《高等数学二》5月22日专为备考2025年高等数学二考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、若，则。（）  

答 案：错

解 析：

单选题

1、设函数f(x)在x=0处连续,g（x）在x = 0处不连续，则在x= 0处（）

• A：f（x）g（x）连续
• B：f（x）g（x）不连续
• C：f（x）＋g（x）连续
• D：f（x）＋g（x）不连续

答 案：D

解 析：f（x）在x=0处连续，g（x）在x=0处不连续，故f（x）＋g（x）在x=0处不连续，否则若f（x）＋g（x）在x=0处连续，则f（x）＋g（x）-f（x）=g（x）在x=0处连续，与题意矛盾，故选D选项.

2、反常积分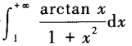等于（）。  

• A：
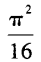
• B：
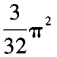
• C：
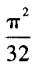
• D：

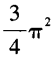
答 案：B

解 析：本题考查的知识点是反常积分的求解。 选B。  

主观题

1、在15件产品中，有2件是次品，另外13件是正品．现从中任取3件产品．求取出的3件产品中：（1）恰有1件是次品的概率；
（2）至少有1件次品的概率．

答 案：解：（1）P（恰有1件次品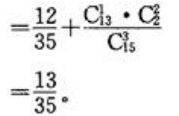）＝（2）P（至少有1件次品）＝P（恰有1件次品）＋P（恰有2件次品）

2、某班有党员10人，其中女党员有6人，现选3人组成党支部．设事件A＝{党支部中至少有1名男党员}，求P（A）．

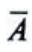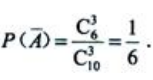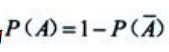答 案：解：＝{党支部中没有男党员}，则因为，所以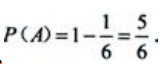

填空题

1、设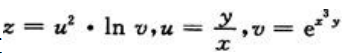，则dz＝（）

答 案：

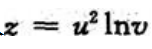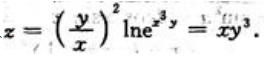解 析：方法一：把u，v代入中，有故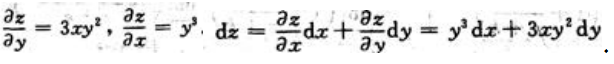方法二：按复合求导法则求导，再代入全微分公式中，。
所以
方法三：利用一阶微分形式的不变性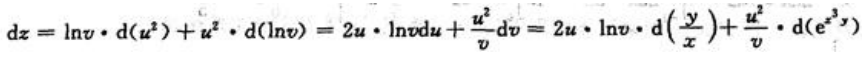

2、设z==（）

答 案：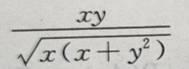

解 析：

简答题

1、计算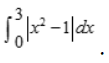  

答 案：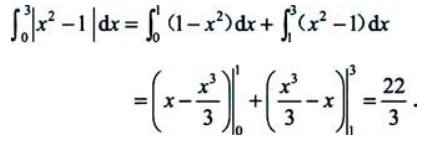

2、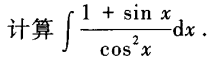  

答 案：本题考查的知识点是不定积分的积分公式及凑微分（即第一换元积分法）的积分方法。